Conditions de maintien vis-à-vis du déversement d’une poutre

De manière générale, une poutre à section en I, fléchie par rapport à son axe de forte inertie, peut présenter un risque de déversement si sa semelle comprimée n’est pas maintenue de façon continue sur sa longueur. Des maintiens latéraux intermédiaires peuvent être prévus afin d’améliorer la résistance au déversement de la poutre. Ce document fournit des informations pour concevoir des maintiens latéraux efficaces.

Principe

Au droit d’une section donnée, une poutre peut être considérée comme maintenue latéralement vis-à-vis de l’instabilité par déversement si le déplacement latéral et la rotation de cette section autour de l’axe de la poutre sont empéchés.

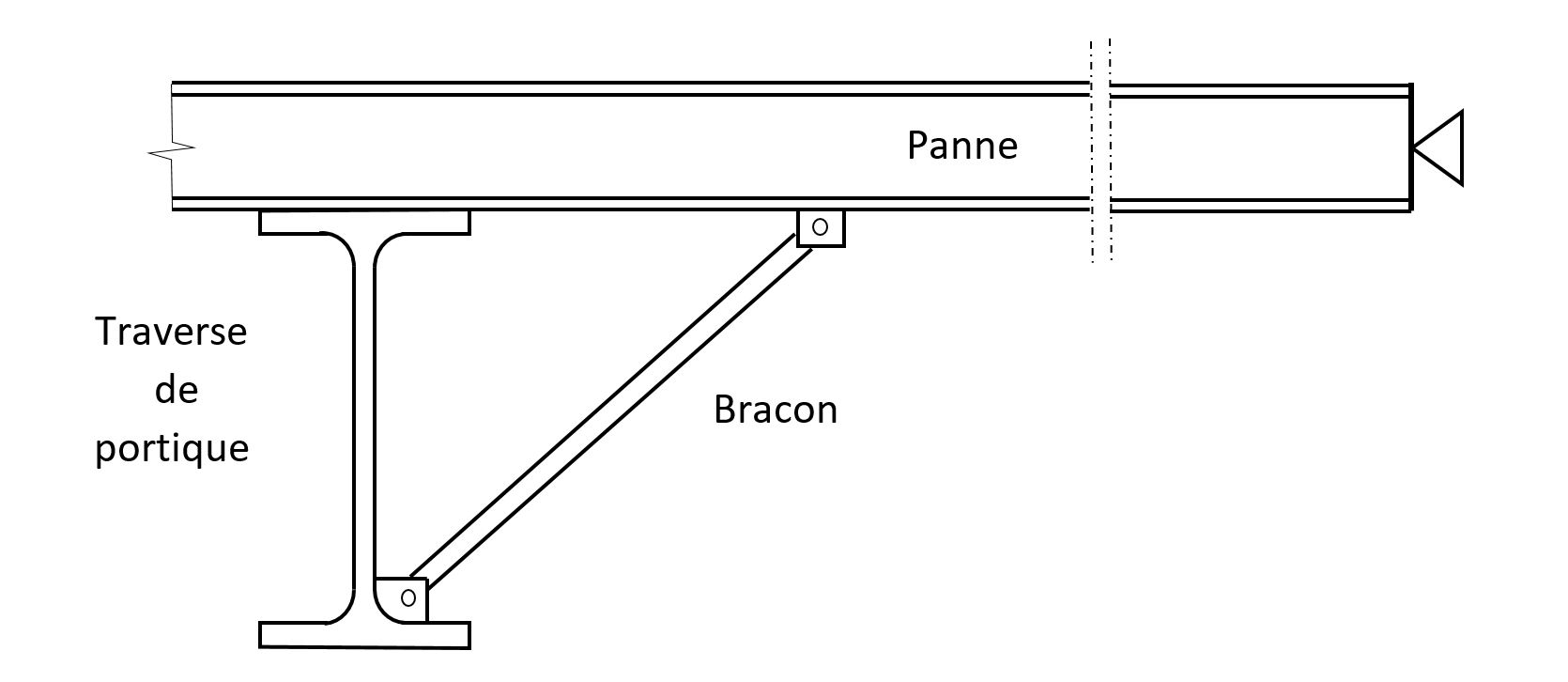
Un exemple typique est celui d’une traverse de portique maintenue latéralement par une panne bloquée en déplacement longitudinal (par exemple, attache à un nœud d’une poutre au vent). La présence d’un bracon s’oppose à la rotation de la section de la traverse en mobilisant la rigidité flexionnelle de la panne.

Quelques idées erronées

Présence d’un raidisseur transversal

Une idée trop répandue consiste à considérer qu’en disposant un raidisseur transversal soudé sur l’âme et les semelles, on peut assurer un maintien de la semelle opposée à la semelle effectivement maintenue en déplacement latéral. Ce raisonnement est totalement erroné car un raidisseur transversal ne peut pas s’opposer à la rotation de la section autour de l’axe de la poutre. Un raidisseur transversal est donc inefficace vis-à-vis du déversement.

Point de moment nul (point d’inflexion)

Une section où le moment de flexion est nul ne peut, en aucun cas, être assimilée à une section maintenue vis-à-vis du déversement. En effet, dans le mode propre d’instabilité, on peut généralement observer un déplacement latéral et une rotation de cette section autour de l’axe de la poutre. Par conséquent, la résistance au déversement doit être vérfiée entre deux sections qui sont réellement maintenues vis-à-vis du déplacement latéral et de la rotation autour de l’axe de la poutre.

Dimensionnement du maintien latéral

Le dispositif local de maintien au déversement peut être dimensionné en considérant un pourcentage de l’effort normal dans la semelle comprimée, appliqué latéralement. Il est d’usage de prendre 2% de cet effort normal (voir §5,23 de l’Additif 80 aux règles CM66 [2]). Dans l’Eurocode 3 Partie 1-1 [1], il est demandé de prendre 2,5% de l’effort normal dans la semelle comprimée au droit d’une rotule plastique (EN 1993-1-1, 6.3.5.2(3)B). Cet effort n’est utilisé que pour une vérification locale (bracon par exemple).

Les efforts de stabilisation se reportent généralement sur un système triangulé (par exemple, une poutre au vent en toiture). Pour le calcul du système triangulé, il convient de se référer au paragraphe 5.3.3 de l’Eurocode 3 Partie 1-1 intitulé « Imperfection pour l’analyse des systèmes de contreventement ». Il n’y a donc pas lieu d’effectuer le cumul des 2% d’effort normal dans les semelles pour déterminer les efforts de stabilisation exercés sur une poutre au vent.

Dans certaines circonstances, il est peut être utile de vérifier que le maintien latéral présente localement une rigidité satisfaisante. L’Eurocode 3 ne fournit pas de critère de rigidité. En revanche, l’Additif 80 aux Règles CM66 (§ 5,23) [2] donne le critère suivant pour la rigidité k de l’appui :

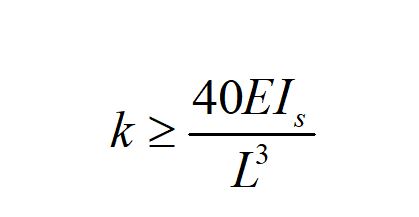
Où :        E     est le module de Young de l’acier

              I_s     est le moment d’inertie de la semelle comprimée, calculé par rapport à l’axe de faible inertie de la section.

              L     est la longueur du tronçon de poutre maintenu au déversement

              k      est la rigidité du maintien latéral qui peut être calculée comme le rapport d’une force F appliquée en ce point au déplacement D qui en résulte. Voir Figure 2.

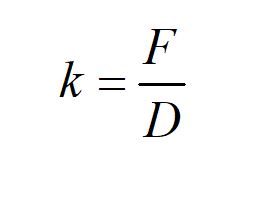
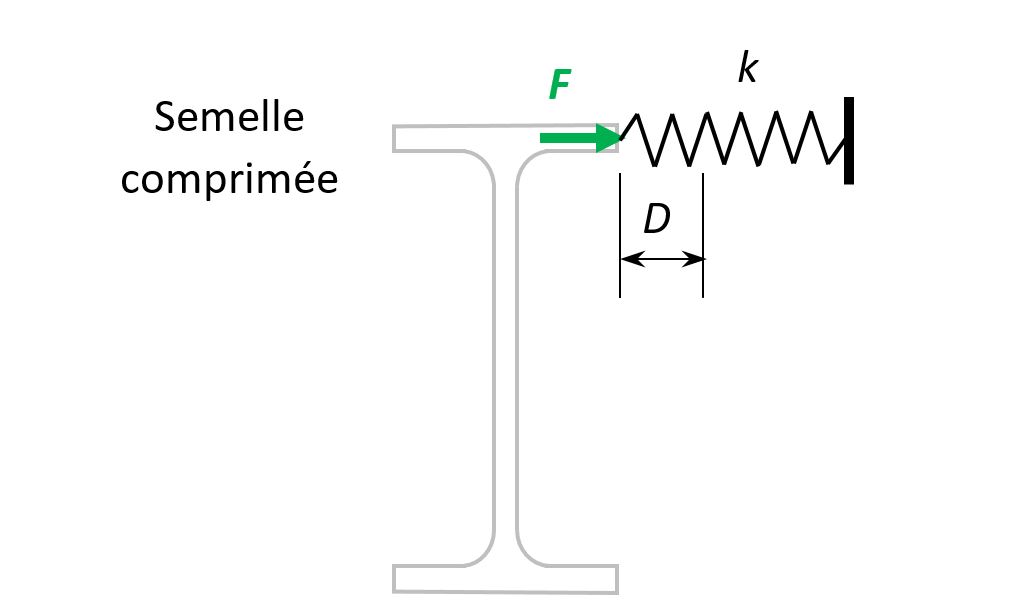
Rigidité d’un maintien par un bracon

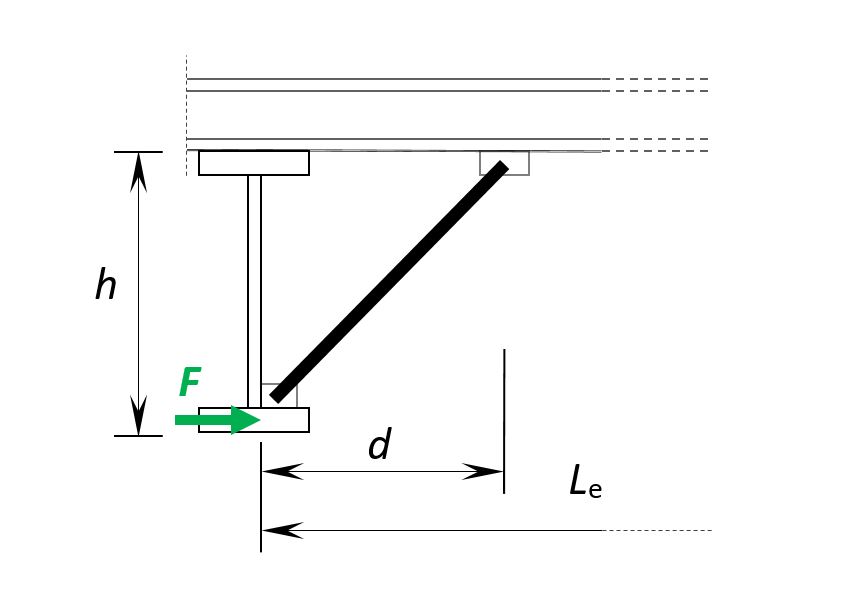
Une expression de la rigidité latérale procurée par un bracon selon le schéma de la Figure 3, est donnée dans l’Additif 80 aux Règles CM66 [2]. La rigidité latérale peut être calculée par l’expression suivante :

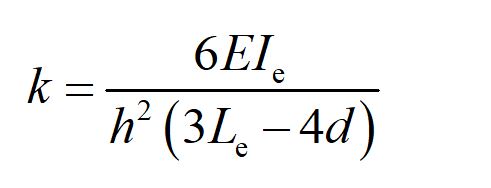
Où :        E est le module de Young de l’acier ;

               I_eest le moment d’inertie de flexion de la panne dans le plan vertical ;

               h est la hauteur de la section transversale ;

               L_e est la distance entre axes des poutres ;

               d est la distance horizontale entre l’axe d’une poutre et l’attache sur la panne.

Références

[1]      NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.

[2]      Additif 80 aux Règles CM66. Revue construction métallique n°1-1981. CTICM.

Télécharger le document

Alain Bureau, chef du service recherche construction métallique , CTICM