Calcul des contraintes de cisaillement dans une section #1

Section rectangulaire pleine – Section circulaire pleine

Les questions posées au CTICM dans le cadre de l’assistance technique montrent que le calcul des contraintes de cisaillement dans une section transversale de poutre n’est pas toujours bien maîtrisé par les calculateurs des bureaux d’études.

Nous proposons donc de présenter la formule générale permettant de calculer les contraintes de cisaillement dans une section et d’en tirer les formules pratiques pour les cas suivants :

• section rectangulaire pleine
• section circulaire pleine.

Les sections rectangulaires et circulaires creuses ainsi que les sections en I, feront l’objet de deux autres articles publiés prochainement.

Rappel de l’expression générale

La contrainte de cisaillement élastique (ou contrainte tangentielle) t peut être déterminée en un point d’une section quelconque soumise à un effort tranchant suivant l’axe z-z, en utilisant l’expression suivante (voir figure n°1) :

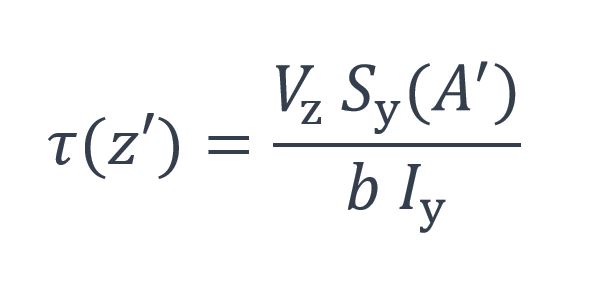
Où :

• z’ est la distance du bord supérieur de la section au point considéré ;
• V_z est l’effort tranchant agissant sur la section étudiée ;
• b est la largeur de la section au niveau du point considéré ;
• S_y est le moment statique par rapport à l’axe y-y de la zone A’ de la section située au-dessus du point considéré ;
• I_y est le moment d’inertie de flexion par rapport à l’axe y-y de la section complète.

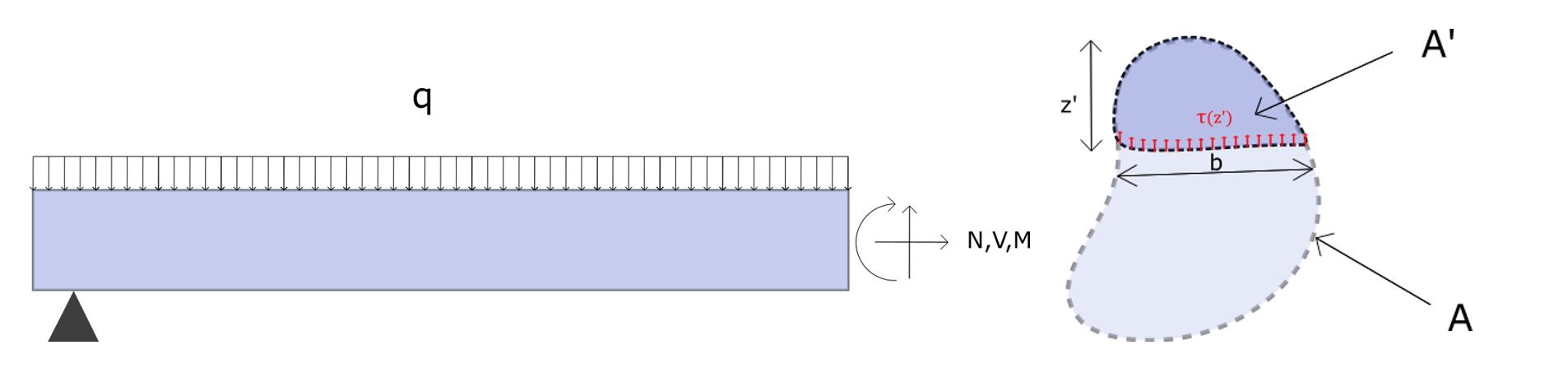
Remarque : à largeur de section égale, la contrainte de cisaillement est maximale au niveau du centre de gravité.

Principe de réciprocité – Théorème de Cauchy

Par application du principe de réciprocité, ou théorème de Cauchy, on déduit que la contrainte de cisaillement perpendiculaire aux bords de la section est nulle. Voir la figure n°2.

Cas n°1 : Cas d’une section rectangulaire pleine

Hypothèses

Considérons une section rectangulaire de dimensions 50 x 100 mm soumise à un effort tranchant vertical V_z = 50 kN.

Les caractéristiques de la section sont les suivantes :

h = 100 mm

b = 50 mm

I_y = bh³/12 = 416,67 x 10⁴ mm⁴

Contraintes de cisaillement

On cherche à exprimer la contrainte de cisaillement à une distance z’ du bord supérieur de la section. Voir Figure n°3.

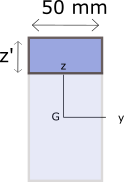
Le moment statique par rapport à l’axe y-y de la section A’ peut être calculé par l’expression suivante :

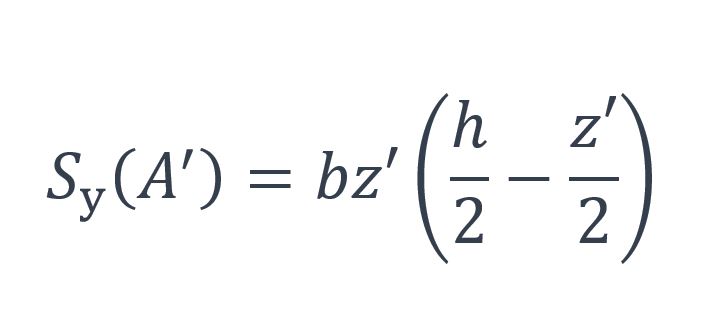
On peut ensuite calculer la contrainte de cisaillement :

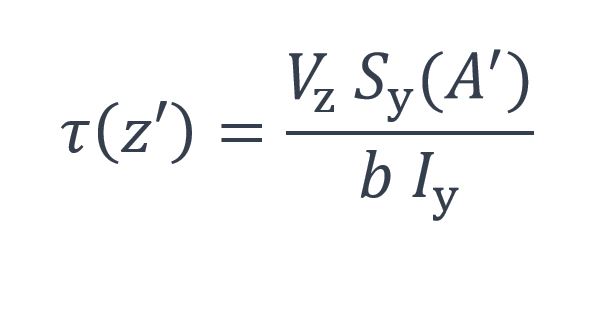
La contrainte de cisaillement est maximale à mi-hauteur :

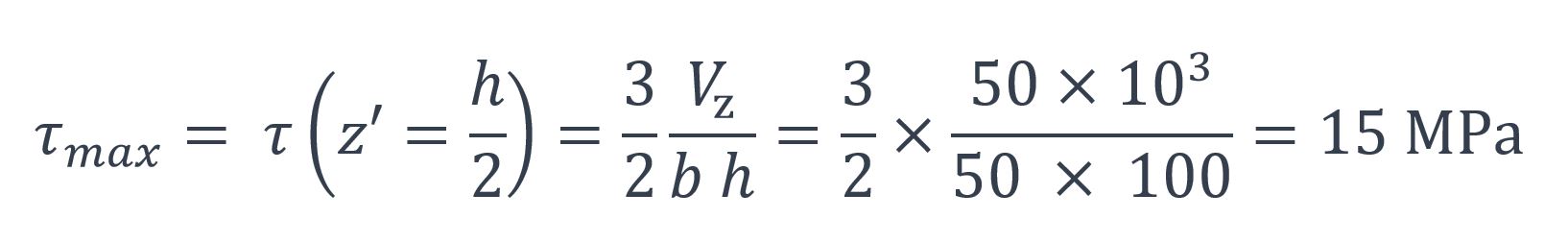
Le diagramme des contraintes de cisaillement est représenté à la Figure n°4.

Cas n°2 : Cas d’une section circulaire pleine

Hypothèses

Considérons une section circulaire de diamètre D = 100 mm soumise à un effort tranchant vertical V_z = 120 kN.

Le moment d’inertie de flexion est calculé à l’aide de l’expression suivante :

I_y = p D⁴/64 = p R⁴/4 = 490,87 x 10⁴ mm⁴

Contraintes de cisaillement

Effectuons une coupe horizontale située à une distance z’ du bord supérieur de la section. Voir figure n°5.

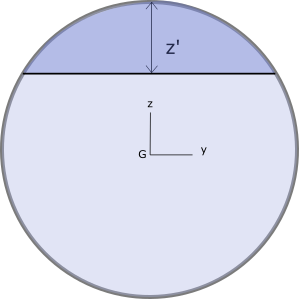
Le moment statique par rapport à l’axe y-y de la coupe s’exprime par :

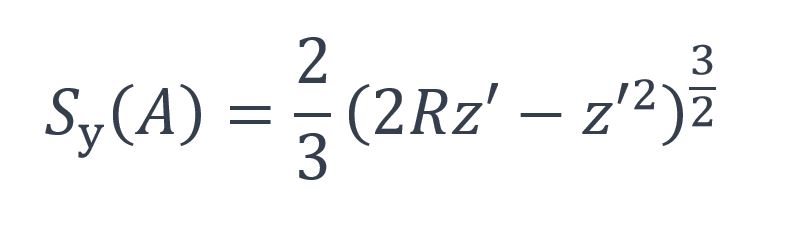
Avec

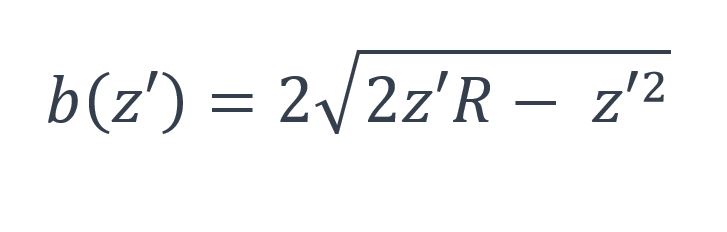
Et donc

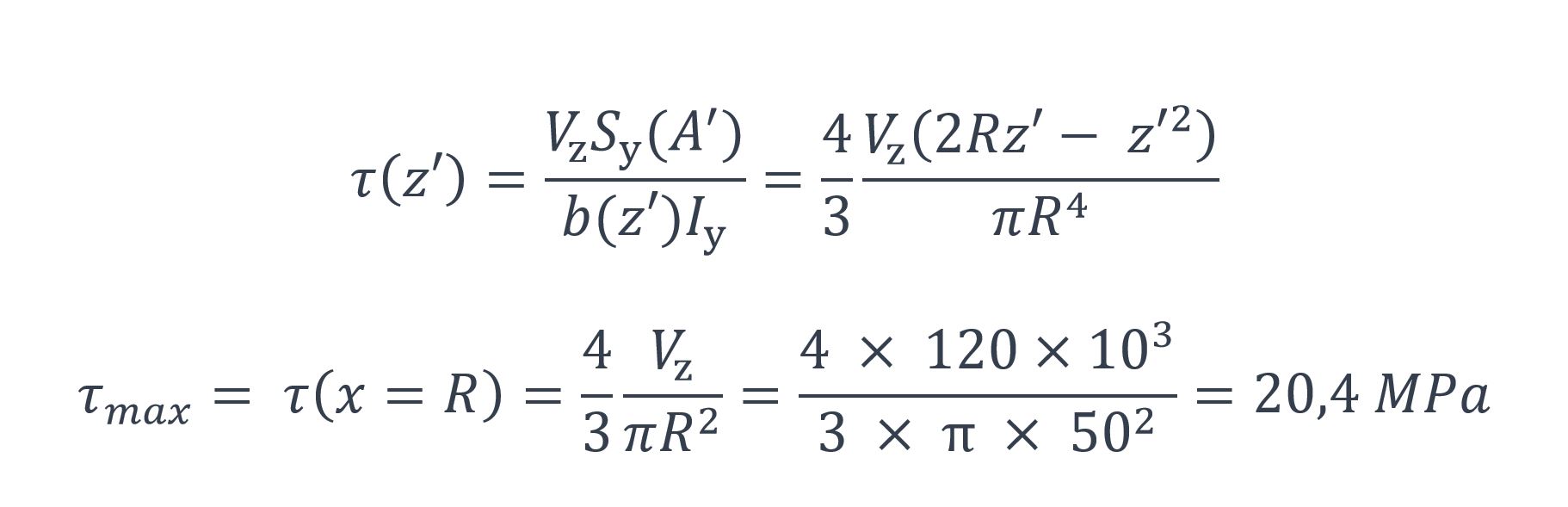
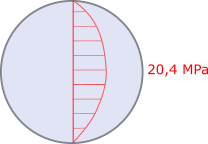
Le diagramme des contraintes de cisaillement est représenté à la figure n°6.

Télécharger le document

Guillaume Delacourt, ingénieur recherche construction métallique – CTICM