Tout savoir sur
la construction métallique
L’Eurocode 3 (NF EN 1993-1-1 [1]) donne toutes les informations nécessaires pour traiter le cas du flambement par flexion des barres comprimées. En revanche, cette norme reste beaucoup plus vague sur l’effet du flambement par torsion et par flexion-torsion qui représente un mode de ruine réel dans certaines situations pour les profilés ouverts.
Cette publication présente le calcul des efforts normaux critiques liés au flambement élastique par torsion et par flexion-torsion. Ce calcul représente la première étape principale d’une vérification de la résistance d’une barre comprimée vis-à-vis de ces modes de flambement. Il est important de noter que le calcul de l’effort normal critique ne dépend pas de la classe de la section. Par conséquent, il convient d’appliquer les formules présentées dans la suite avec les caractéristiques de section brute non réduites par l’effet éventuel du voilement.
En fonction du type de la section, la détermination de la résistance au flambement doit être effectuée conformément au paragraphe 6.3.1.4 de l’Eurocode 3 Partie 1-1 [1] pour les sections laminées et les sections soudées ou conformément au paragraphe 6.2.3 de l’Eurocode 3 Partie 1-3 [2] pour les sections formées à froid.
Les sections doublement symétriques et les sections symétriques par rapport à un point, comme celles montrées à la Figure 1, peuvent être sensibles au flambement par torsion. Ces sections ont en commun que le centre de gravité G est confondu avec le centre de cisaillement S.
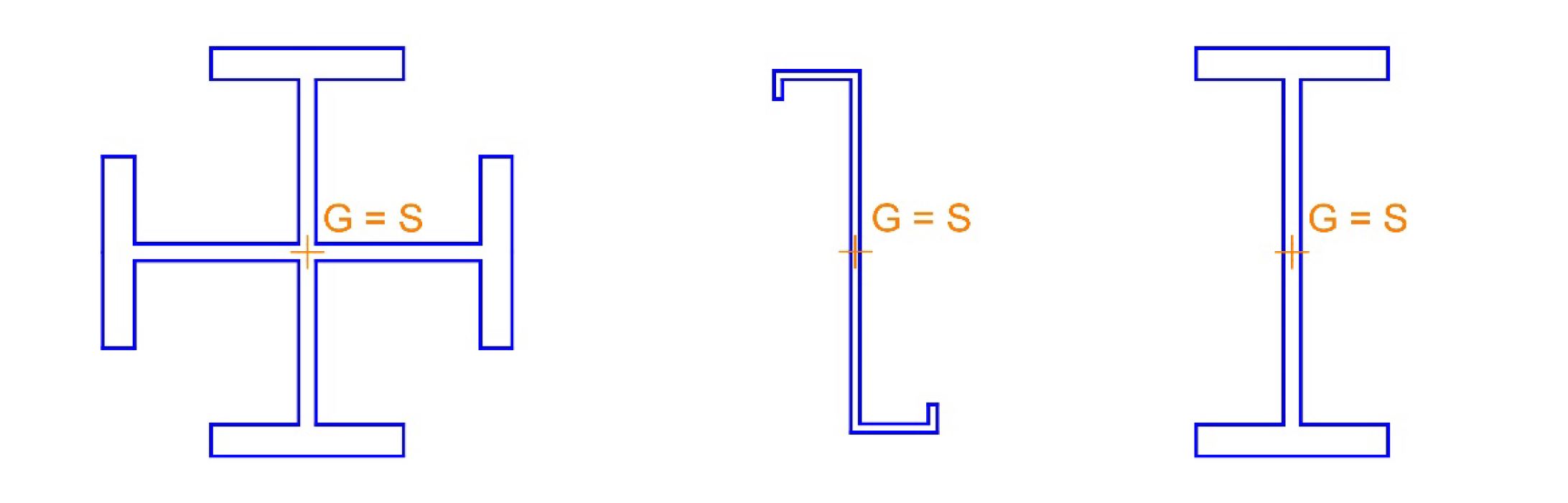
On peut noter que les sections en I doublement symétriques sont uniquement sensibles au flambement par torsion si la longueur de la barre est relativement faible ou si la longueur de flambement autour de l’axe de faible inertie (mesurée entre deux maintiens en déplacement latéral) est plus faible que la longueur de flambement par torsion (mesurée entre deux maintiens en rotation par torsion) – des informations plus détaillées sont données dans les références [3] et [4].
Pour les sections de la Figure 1, on peut calculer l’effort normal critique pour le flambement par torsion Ncr,T avec la formule suivante :
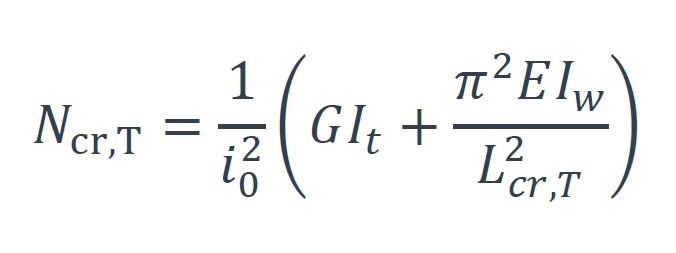
où :
i0 : est le rayon de giration polaire
G : est le module de cisaillement
It : est l’inertie de torsion
E : est le module de Young
Iw : est l’inertie de gauchissement
Lcr,t : est la longueur de flambement par torsion
Généralement, on doit considérer la longueur d’épure comme longueur de flambement par torsion d’une barre simplement appuyée à ses extrémités (voir aussi référence [3].
Contrairement aux sections de la Figure 1, les sections mono-symétriques, dont quelques exemples sont montrés à la Figure 2, sont sujettes au flambement par flexion-torsion. Ce mode de flambement combine un flambement par flexion autour de l’axe de symétrie et un flambement par torsion.
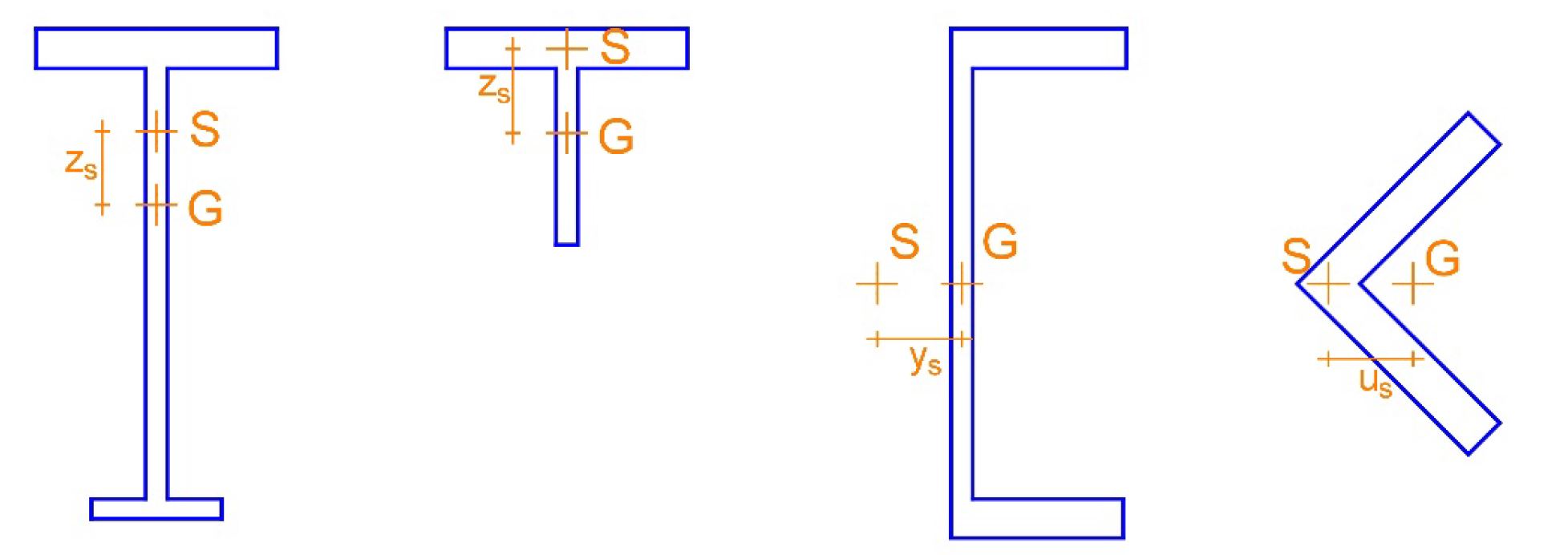
En fonction de la forme de la section, l’effort normal critique de flambement par flexion-torsion est donné par :
Sections symétriques par rapport à l’axe de faible inertie z-z (par exemple section en I mono-symétrique) :
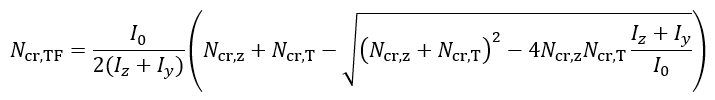
Sections symétriques par rapport à l’axe de forte inertie y-y (par exemple section en U) :
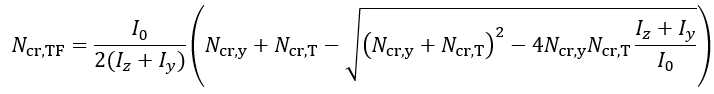
Cornières à ailes égales :
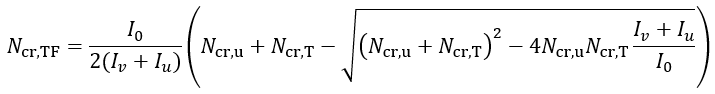
où :
I0 : est l’inertie polaire
Iz, Iy, Iv, Iu : sont les inerties autour de l’axe z, y, v et u (voir EN 1993-1-1 pour la définition des axes)
Ncr,z, Ncr,y, Ncr,u : sont les efforts critiques de flambement par flexion autour de l’axe z, y et u respectivement.
Pour les sections asymétriques, il n’existe pas de solution « simple » et il est nécessaire de calculer l’effort normal critique de flambement par flexion-torsion en déterminant la plus petite racine de l’équation cubique en N suivante :
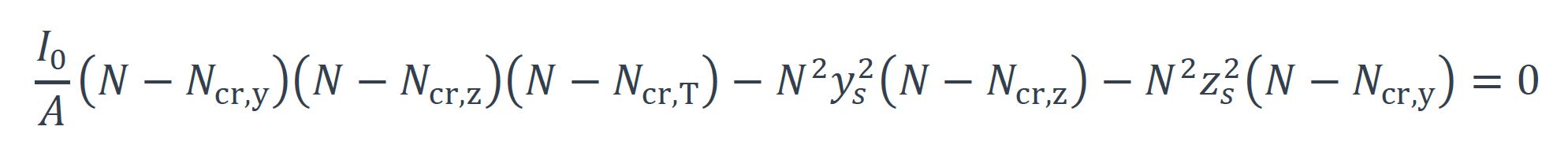
où :
A : est l’aire de la section transversale
Récapitulatif
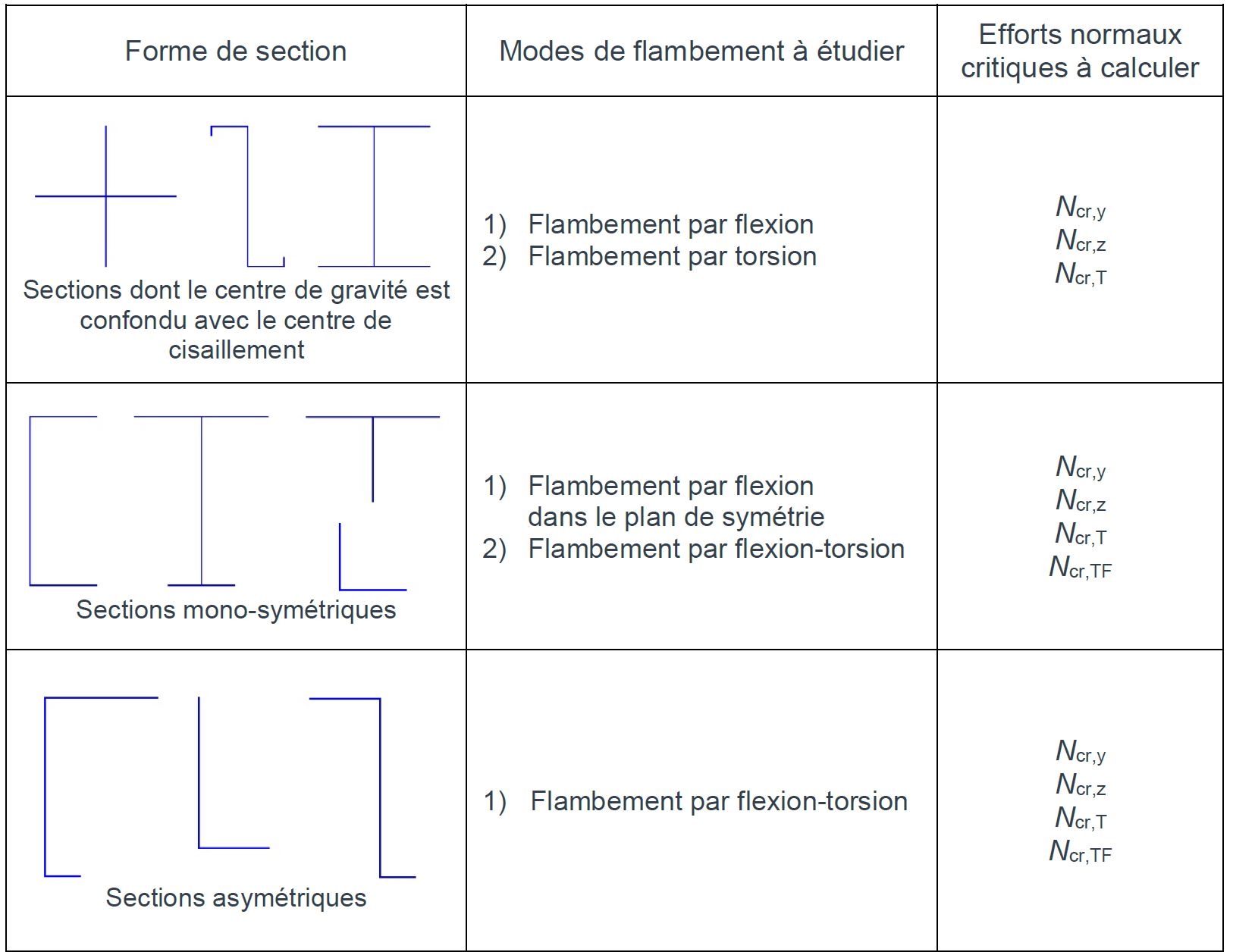
Le Tableau 1 récapitule les modes de flambement à étudier en fonction de la forme de section.
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[2] NF EN 1993-1-3 : Eurocode 3 – Calcul des structures en acier. Partie 1-3 : Règles générales – Règles supplémentaires pour les profilés et plaques formés à froid. AFNOR. Octobre 2006.
[3] Bureau A., Flambement par torsion et par flexion-torsion d’une barre comprimée. Revue Construction Métallique, 2004/2.
[4] S. P. Timoshenko et J. M. Gere. Theory of elastic stability. 2nd edition. McGraw-Hill. 1961.
André Beyer, chef de projet recherche – CTICM