Résistance au flambement d’un poteau courbe
La partie 1-1 de l’Eurocode 3 [1] contient des règles pour la vérification de la résistance au flambement des barres droites. Ce document propose une approche simple pour vérifier la résistance au flambement d’un poteau présentant une courbure, selon les principes de l’Eurocode 3.
Domaine d’application
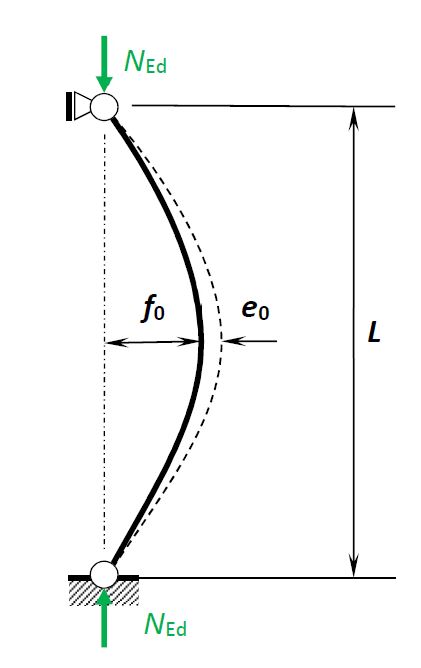
La méthode décrite dans ce document s’applique à un poteau courbe de flèche nominale f0, soumis à un effort de compression suivant l’axe passant par les appuis, comme présenté à la Figure n°1.
La barre doit avoir une section transversale de classe 1 sous compression uniforme dans la section, de façon à pouvoir développer des déformations plastiques importantes sans risque de voilement local des parois.
Ce document ne couvre que la résistance au flambement par flexion dans le plan du poteau courbe dont la flèche nominale f0 ne doit pas excéder L/10. La vérification de la stabilité hors plan n’est pas couverte par ce document et pourra faire l’objet d’une publication ultérieure.
La méthode proposée pourrait être appliquée à un poteau nominalement droit qui présente un défaut de rectitude supérieur à la tolérance essentielle imposée par la norme NF EN 1090-2 [2], en prenant comme flèche f0 la valeur mesurée du défaut de rectitude.
Considérations préliminaires
Une barre courbe peut être obtenue par cintrage à froid à l’aide d’un système approprié. Cette opération engendre des contraintes normales qui se superposent aux contraintes
résiduelles initiales générées lors de la fabrication de la barre droite. A l’issue de cette opération, la barre a subi des déformations plastiques importantes et est le siège d’un nouvel état de contraintes normales auto-équilibrées dans la section transversale. Ces contraintes ont une influence significative sur la résistance de la barre vis-à-vis des phénomènes d’instabilité (flambement, déversement, voilement).
Le niveau des contraintes normales résiduelles à l’issue du cintrage dépend de nombreux paramètres : géométrie de la section, limite d’élasticité, rayon de courbure, etc. Il est donc difficile d’estimer a priori le niveau de ces contraintes et leur répartition dans la section. En conséquence, il convient de se placer du côté de la sécurité en se référant à la courbe d pour la vérification de la résistance au flambement.
Le principe de la méthode est d’ajouter une imperfection géométrique d’amplitude e0 à la flèche nominale f0 de la barre cintrée, comme représenté à la Figure n°1.
Il convient de noter que la référence [3] fournit de nombreuses informations relatives à la conception et à la fabrication de poutres courbes.
Méthode de vérification
Etape n°1 : Charge axiale critique Ncr
Pour une barre courbe de flèche nominale inférieure à L/10, la formule d’Euler reste applicable (avec une erreur inférieure à 3%) :
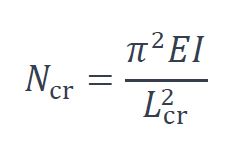
Où :
E est le module de Young (E = 210000 MPa pour l’acier) ;
I est le moment d’inertie de flexion de la section ;
Lcr est la longueur de flambement qui peut être prise égale à L. pour une barre articulée à ses deux extrémités.
Etape n°2 : imperfection locale de la barre
L’imperfection e0 peut être obtenue à partir du Tableau 5.1 de l’Eurocode Partie 1-1, en considérant la courbe d : e0 = L/150 (colonne « Analyse élastique »).
Etape n°3 : moment de flexion maximal
Le moment de flexion maximal doit être calculé en tenant compte de l’imperfection locale de la barre et de l’amplification par les effets du second ordre, à l’aide de l’expression suivante:
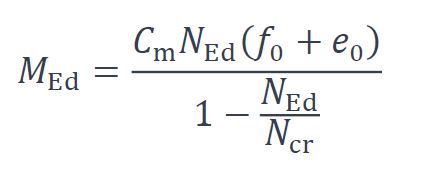
Où :
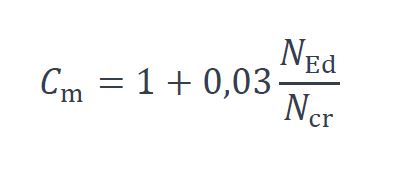
Etape n°4 : résistance de la section la plus sollicitée
La résistance de la section doit être vérifiée selon le critère de résistance élastique suivant:
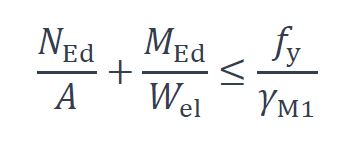
Références
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[2] NF EN 1090-2 : Exécution des structures en acier et des structures en aluminium. Partie 2 : exigences techniques pour les structures en acier. AFNOR. Juin 2018.
[3] Design of curved steel by C. King and D. Brown. Publication 281. The Steel Construction Institute. 2001.
Alain Bureau, chef du service recherche construction métallique , CTICM