Réponse vibratoire d’une poutre sous la charge dynamique induite par la marche #1
Partie 1: Méthodologie
Cet article présente une méthode simplifiée pour étudier la réponse dynamique d’une poutre soumise à un chargement concentré représentant la marche d’une personne. La réponse ainsi obtenue peut constituer la base d’une éventuelle évaluation du confort vibratoire des utilisateurs de la structure.
Caractéristiques de la structure
La structure étudiée est une poutre simplement appuyée, satisfaisant les conditions de Navier-Bernoulli (petites perturbations, déformations sur la ligne moyenne, principe de Saint-Venant, matériau linéairement élastique, homogène et isotrope) et ayant un amortissement proportionnel à la vitesse de sa déformation.
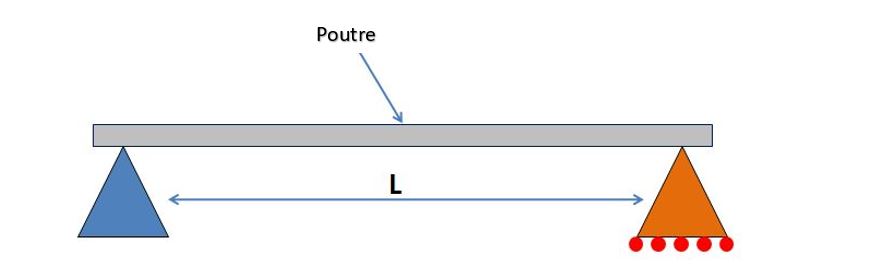
Les caractéristiques de la poutre nécessaires pour l’étude dynamique sont :
- Sa portée L (en m)
- Sa masse linéique m (en kg/m)
- Sa raideur flexionnelle El (en N.m²)
- Son coefficient d’amortissement
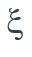 (dont la valeur est usuellement comprise entre 0,2 % et 3 %)
(dont la valeur est usuellement comprise entre 0,2 % et 3 %)
On considère que la poutre est au repos avant l’application de la charge.
Caractéristiques de la charge
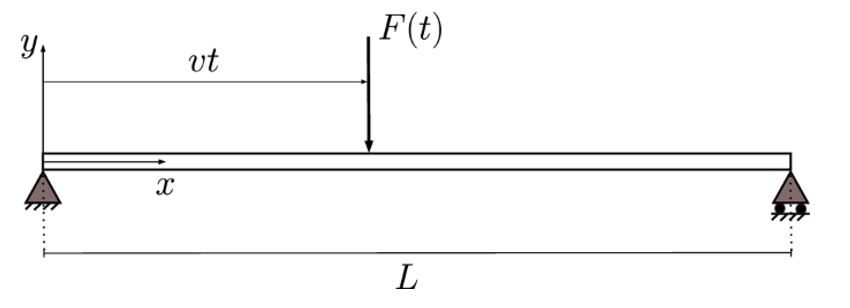
On suppose que la poutre est soumise à un chargement mobile résultant de la marche d’une personne. Ce chargement peut être décomposé en série de Fourier selon la formule classique :
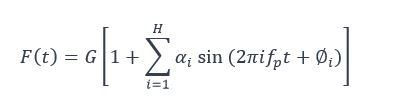
où :
- G est le poids de la personne (en N)
- fp est la fréquence de marche (en Hz)
- H est le nombre d’harmoniques considéré
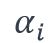 est le coefficient de Fourier du ie harmonique
est le coefficient de Fourier du ie harmonique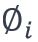 est le déphasage du ie harmonique
est le déphasage du ie harmonique
La fréquence de marche fp est souvent comprise entre 1,5 Hz et 2,5 Hz [2]. De plus, on suppose que la personne se déplace avec une vitesse 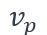 constante tout au long du mouvement. De ce fait, la charge sera présente sur la poutre pendant une durée
constante tout au long du mouvement. De ce fait, la charge sera présente sur la poutre pendant une durée 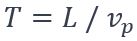 (en s).
(en s).
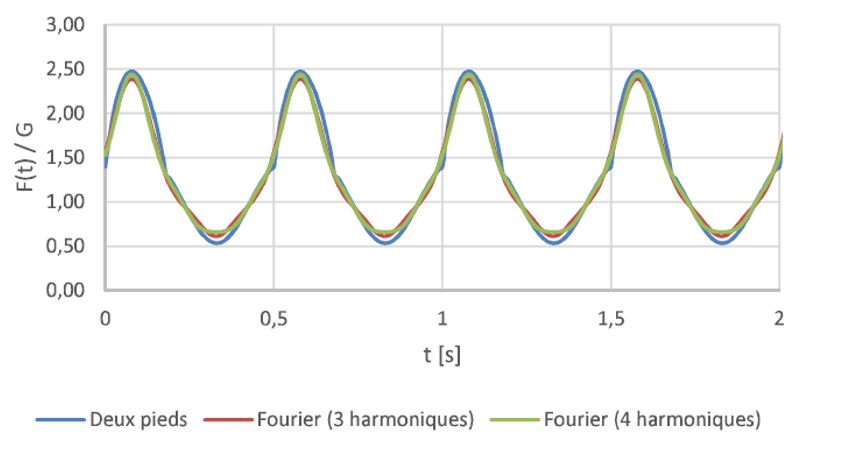
Le graphe suivant présente l’évolution d’une charge de marche réelle ayant une fréquence fp=2 Hz, comparée avec celle donnée par l’équation (1) pour 3 et 4 harmoniques, et normalisée par rapport au poids :
Paramètres de base
On définit trois pulsations de base ( 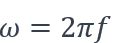 en rad/s) qui seront utilisées dans l’étude dynamique :
en rad/s) qui seront utilisées dans l’étude dynamique :

Domaine et conditions d’application
La méthode présentée ci-après s’applique aussi bien aux poutres supportant des passerelles piétonnes qu’aux poutres structurelles des bâtiments ayant divers usages (hôpitaux, résidences, bureaux, écoles, ateliers, etc.).
Les conditions d’application de la méthode sont les suivantes :
- L’étude est limitée au cas des vibrations verticales de la poutre.
- On doit avoir
 .
.
On peut distinguer pour le mouvement vibratoire de la poutre les deux phases suivantes :
- Phase d’excitation, se produisant pendant toute la durée T.
- Phase de vibration libre, se produisant après disparition de la charge.
On se contente d’étudier la réponse uniquement pendant la phase d’excitation, car la phase de vibration libre présente, dans presque tous les cas vibratoires, des réponses beaucoup plus faibles qui peuvent être négligées.
Méthode simplifiée d’étude de réponse
Il s’agit d’une méthode permettant de déterminer de manière approchée la réponse en déplacement de la poutre, en calculant séparément la réponse de la composante statique du chargement humain d’une part et celle de ses composantes sinusoïdales d’autre part. Les réponses associées sont détaillées ci-après.
Réponse sous l’effet de la partie constante du chargement
On considère que la poutre est soumise à une charge mobile d’intensité constante . Le calcul dynamique est basé sur l’approximation de la formule exacte (1.24) de la référence [1] (page 18) en se limitant au premier terme de la somme et en utilisant les conditions d’application citées plus haut.
La réponse en déplacement de la poutre au niveau d’une section d’abscisse x (en m) est ainsi obtenue par la formule suivante :
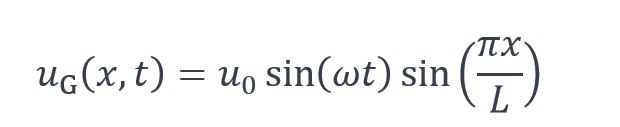
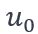 étant la flèche statique de la poutre (en m) sous la charge G:
étant la flèche statique de la poutre (en m) sous la charge G:
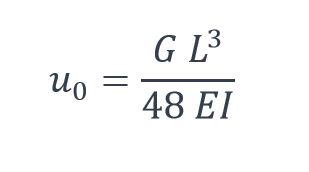
où :
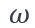 est la pulsation caractéristique de passage.
est la pulsation caractéristique de passage.
L est la portée de la poutre.
El est la raideur flexionnelle de la poutre.
Réponse sous l’effet de la partie sinusoïdale du chargement
On considère que la poutre est soumise à une charge mobile sinusoïdale 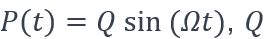 , étant l’amplitude de la charge (en N).
, étant l’amplitude de la charge (en N).
Le calcul dynamique est basé sur l’approximation de la formule exacte (2.6) de la référence [1] (page 34) en se limitant au premier terme de la somme et en utilisant les conditions d’application citées plus haut.
La réponse en déplacement de la poutre est ainsi obtenue par la formule suivante :
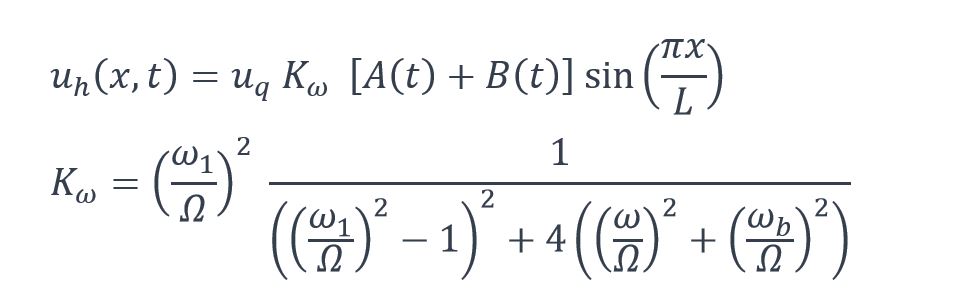
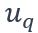 étant la flèche statique de la poutre (en m) sous la charge
étant la flèche statique de la poutre (en m) sous la charge 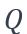 (calculée comme en (3)).
(calculée comme en (3)).
Les fonctions A(t) et B(t) présentant le caractère temporel de la réponse vibratoire sont données par les expressions suivantes :
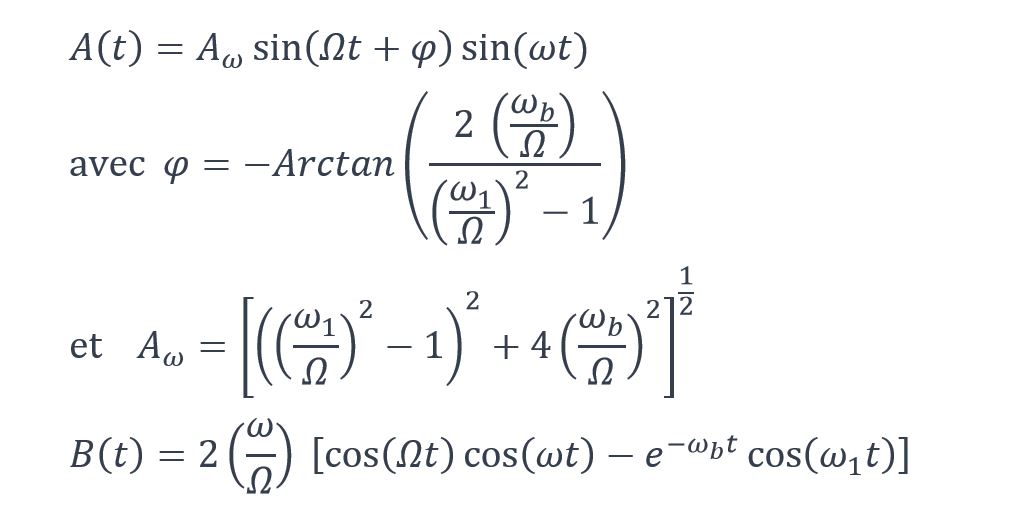
Un cas particulier remarquable est celui de la résonance (où 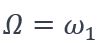 ), dans lequel la formule (4) est largement simplifiée par application de la règle de l’Hospital :
), dans lequel la formule (4) est largement simplifiée par application de la règle de l’Hospital :
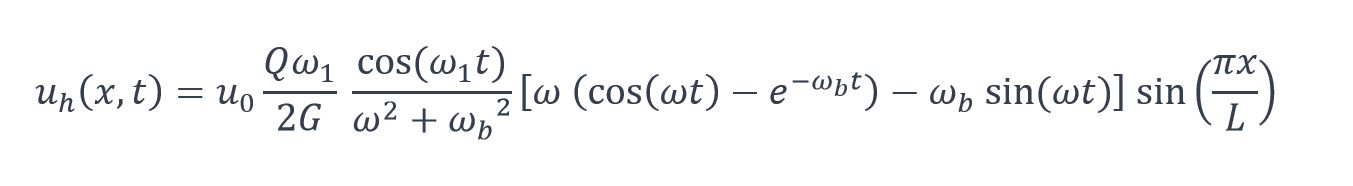
Réponse finale en déplacement
La réponse de la poutre par rapport au chargement représentant la marche d’une personne 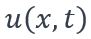 est obtenue en superposant :
est obtenue en superposant :
- La réponse de la partie constante
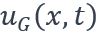 .
. - La réponse de chaque harmonique de marche
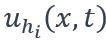 , ayant comme amplitude
, ayant comme amplitude 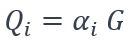 et comme pulsation
et comme pulsation  .
.
La réponse finale est donc :
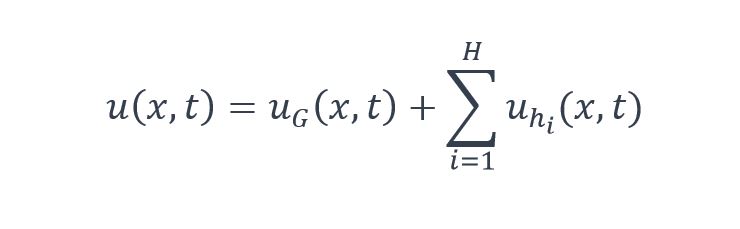
Réponse finale en accélération
Afin de déterminer la réponse de la poutre en accélération, on dérive deux fois les deux formules (1.24) et (2.6) de la référence [1], puis on les simplifie par troncature de la somme au premier terme (correspondant au mode fondamental de vibration) et par usage des conditions d’application citées plus haut. La somme des deux formules obtenues donnera la réponse finale. Ces développements théoriques dépassent le cadre de cet article.
L’usage principal de la réponse en accélération serait d’évaluer le confort de la structure par rapport à ses occupants sous une action de marche d’une personne avoisinante, en utilisant des normes d’appréciation de confort dont figure principalement la norme NF EN ISO 10137. Un exemple détaillé d’évaluation de confort basé sur cette norme sera fourni dans un second article du blog.
Références
[1] L. Fryba, Vibration of solids and structures under moving loads, 1992.
[2] H. Bachmann, W. Ammann, Vibrations in structures induced by man and machines
Youssef El Asri, ingénieur thésard, CTICM


