Déversement élastique des poutres-consoles

Cet article présente une méthode simplifiée pour déterminer le moment critique de déversement élastique des poutres-consoles en s’appuyant sur la référence [1]. L’étude concerne les poutres simplement fléchies à section uniforme et doublement symétrique. A l’encastrement, le gauchissement est cependant supposé libre car il est généralement difficile de justifier d’un blocage complet en gauchissement. En dehors de l’appui, la poutre est libre de déverser sur toute sa longueur.

S’il est montré que le gauchissement est totalement bloqué à l’encastrement, la référence [1] peut être consultée. Si la raideur du maintien au gauchissement à l’appui est connue ou si la poutre étudiée n’entre pas dans le domaine d’application défini, il est conseillé d’utiliser l’un des logiciels LTBeam ou LTBeamN pour évaluer le moment critique de déversement.

Expression du moment critique

La valeur du moment critique de déversement est déterminée par :

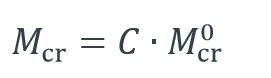
Où M_cr⁰ est le moment critique de déversement de la poutre supposée sur appuis à fourche et soumise à un moment de flexion dans son plan de forte inertie, constant sur la longueur de la poutre, en supposant nulle sa rigidité de gauchissement (EI_w = 0), calculé par :

Le facteur C permet de prendre en compte la rigidité en gauchissement de la poutre, la forme du diagramme de moment, et la possibilité d’appliquer un chargement transversal hors du centre de cisaillement.

Paramètres influençant la valeur du coefficient C

Pour un cas de charge donné, le facteur global C dépend des deux paramètres suivants :

Le paramètre κ_wt prend en compte les propriétés en torsion uniforme et non-uniforme de la section et le paramètre η introduit l’effet stabilisant ou déstabilisant d’un chargement transversal appliqué au-dessus ou en-dessous du centre de cisaillement.

NOTE: La section étant doublement symétrique, le centre de cisaillement est confondu avec le centre de gravité.

Par convention, η est négatif lorsque le chargement a un effet stabilisant (chargement dirigé vers l’extérieur de la section) et il est positif si le chargement a un effet déstabilisant (chargement dirigé vers le centre de cisaillement).

Coefficient C pour différents cas de chargement simples

Le coefficient C a été évalué à l’aide du logiciel LTBeam pour différentes combinaisons des paramètres κ_wt (0 ≤ κ_wt ≤ 1) et η ( -2 ≤ η ≤ 3 ). La valeur de C est donnée dans le tableau suivant tiré de la référence [1] en fonction du chargement :

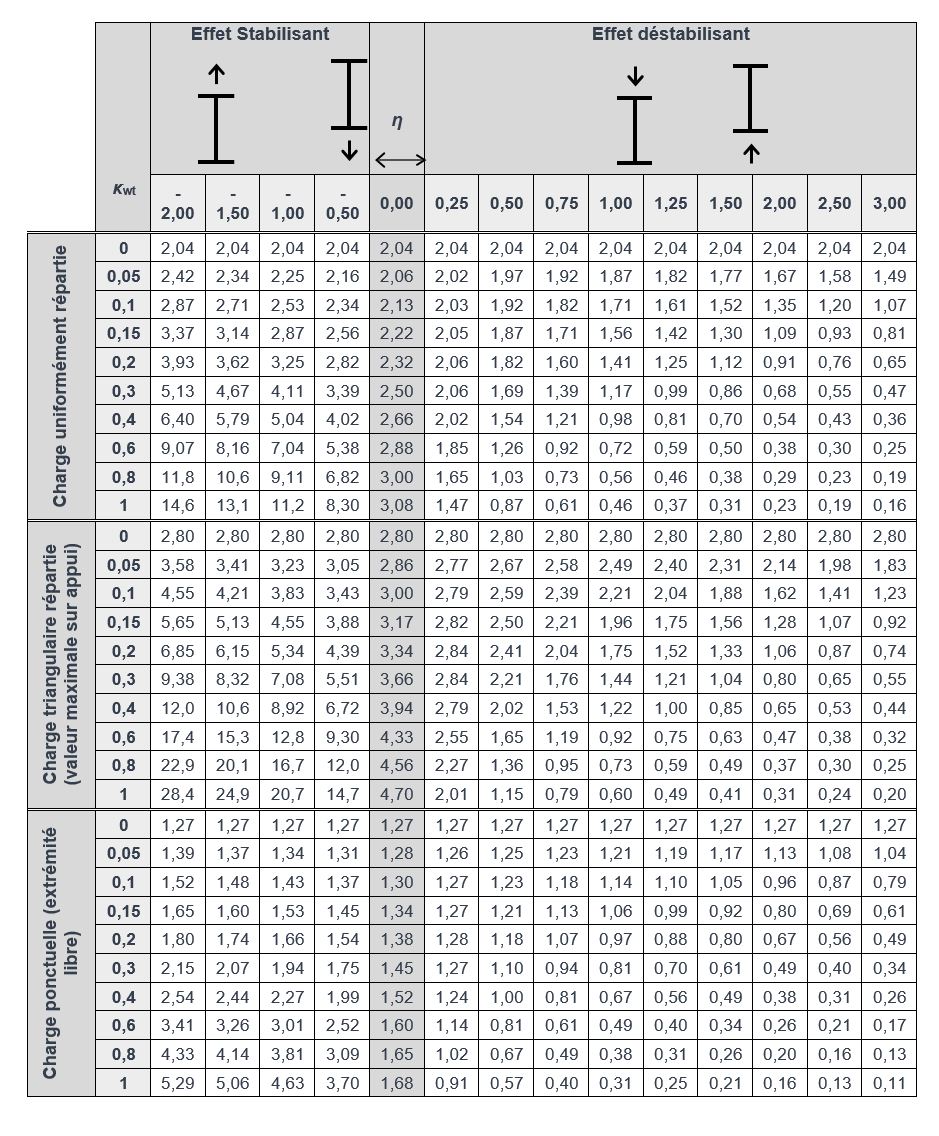
Coefficient C pour une combinaison de charges uniforme et ponctuelle

Lorsqu’une poutre console est simultanément soumise à une charge uniformément répartie q sur sa longueur et une charge ponctuelle F appliquée à l’extrémité libre, la référence [1] propose de déterminer le coefficient C en utilisant la formule d’interaction suivante :

Cette expression est applicable uniquement lorsque les deux conditions suivantes sont réunies :

• Les deux charges q et F agissent dans le même sens ;
• Le signe de η est le même pour les deux charges.

Exemple d’application

L’exemple d’application concerne un IPE 450 de 5m de long soumis à une charge q uniformément répartie sur sa semelle supérieure :

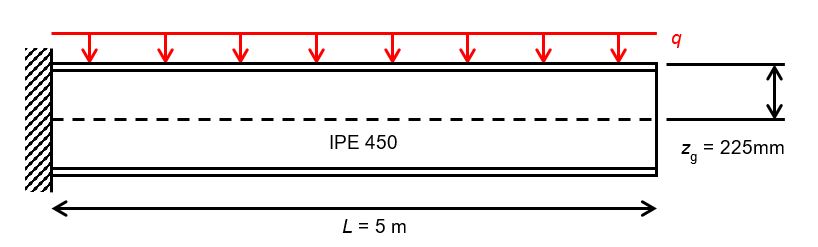
Pour un IPE 450 :

• I_z = 1675,6 cm⁴
• I_t = 66,18 cm⁴
• I_w = 794 246 cm⁶

Les paramètres κ_wt et sont η calculés :

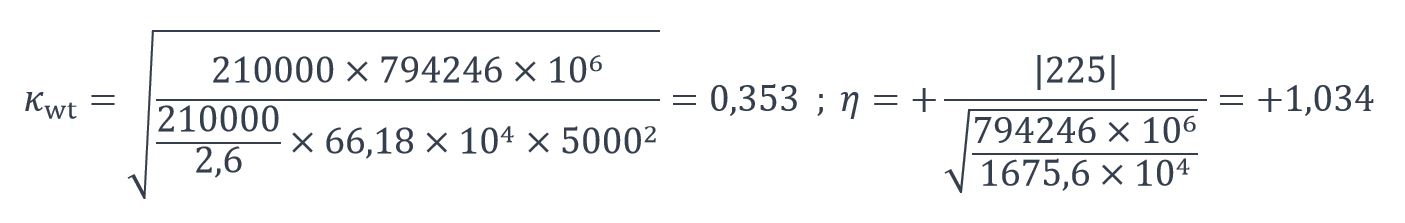
Après une double interpolation linéaire entre les valeurs de C pour κ_wt = 0,3 et κ_wt = 0,4, et pour  η = 1,00 et η = 1,25 tirées du tableau précédent, on obtient : C=1,045 .

Le moment M_cr⁰ est calculé :

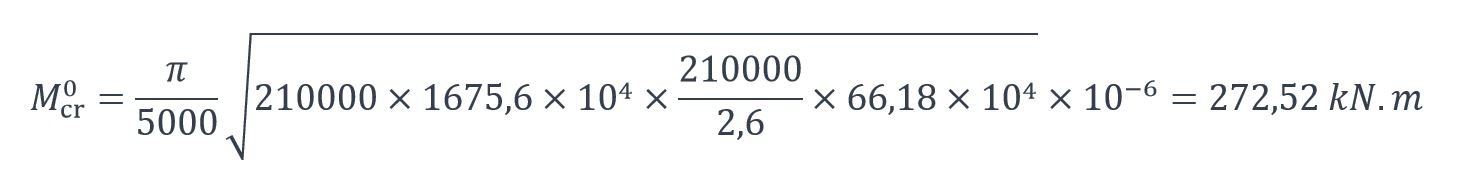
Le moment critique de déversement de la poutre-console vaut finalement :

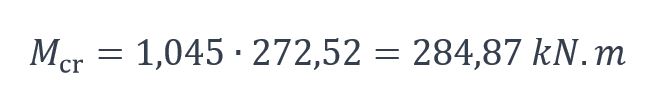
Le calcul mené avec logiciel LTBeamN conduit à : M_cr,LTBN = 282,52 kN.m. L’écart avec le modèle analytique est inférieur à 1%.

Références

[1] Galea, Y. Moment critique de déversement élastique des poutres-consoles à extrémité entièrement libre. Revue construction métallique n°3-2005.

Télécharger le document

Maxime Lebastard, ingénieur de recherche – CTICM