Soudure âme-semelle de PRS #1 – Fonctionnement et sollicitations

Les soudures âme-semelle des profilés reconstitués soudés (PRS) doivent faire l’objet de vérification par référence à l’Eurocode 3 partie 1-8 [1]. Ce premier article d’une série de quatre, décrit le fonctionnement de ces cordons de soudure et les sollicitations auxquelles ils sont soumis. Trois autres articles concernant les soudures âme semelle de PRS seront prochainement publiées sur Métalétech :

• Soudure âme-semelle de PRS – Méthode de dimensionnement
• Soudure âme-semelle de PRS – Effet d’une charge transversale
• Soudure âme-semelle de PRS – Exemple de calcul

Comportement des poutres constituées d’éléments distincts

Une poutre fléchie peut être constituées par des éléments distincts disposés en « couches » successives. La Figure 1 ci-dessous montre deux cas de figure pour une telle poutre sur deux appuis simples :

• les différents éléments sont simplement posés les uns sur les autres, sans liaisons (a)
• les différents éléments sont liés entre eux, sans déplacement différentiel possible (b)

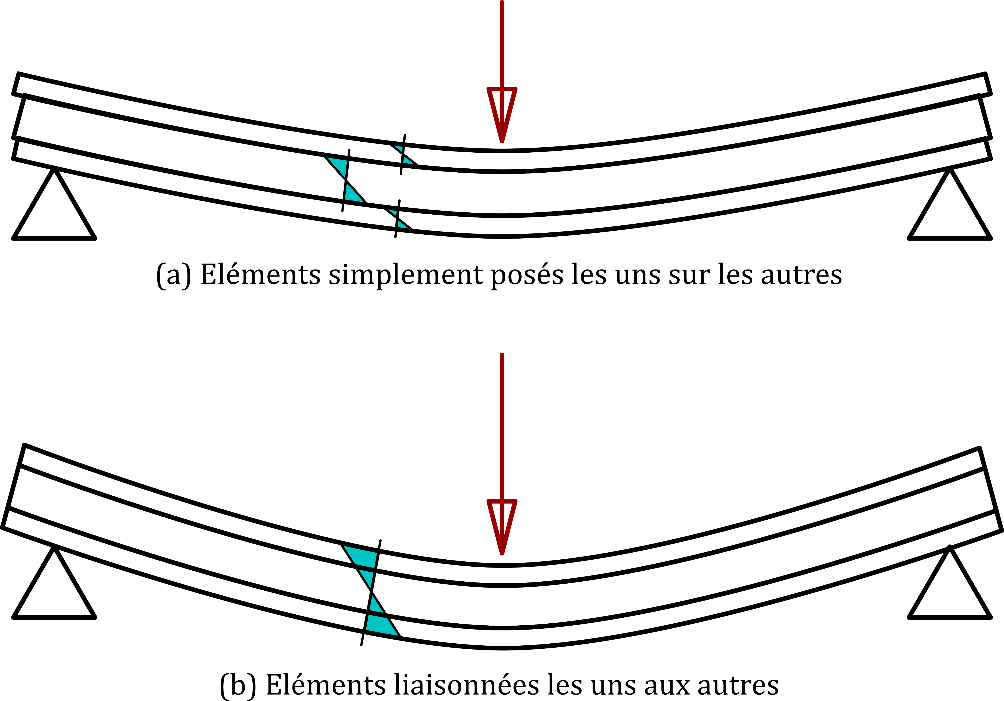
Lorsque les éléments sont simplement posés les uns sur les autres, chaque élément va se comporter en flexion de façon isolée. La contrainte dans les différents éléments se détermine au prorata des inerties. On peut constater que les extrémités de chaque élément se décalent : ils glissent les uns par rapport aux autres.

A contrario, lorsque les éléments sont liaisonnés entre eux, ces derniers vont travailler ensemble et on ne constate pas de décalage aux extrémités. Dans ce cas, la charge est reprise en flexion par la section complète reconstituée et la contrainte se détermine sur la base de l’inertie globale, qui est sensiblement plus élevée que la somme des inerties des éléments séparés.

Dans le cas des profilés reconstitués par soudage (PRS), les différents éléments correspondent aux deux semelles et à l’âme (ou les âmes dans le cas de poutres-caisson). La soudure empêche tout déplacement différentiel entre l’âme et la semelle, permettant ainsi un fonctionnement de la section dans sa globalité. C’est cet effort correspondant au blocage du glissement des plats les uns par rapport aux autres qui doit être repris par la soudure âme-semelle.

Ce type de liaison entre éléments distincts, permettant d’obtenir un meilleur comportement en flexion, est utilisé dans bien d’autres situations. En particulier, c’est le même phénomène à l’origine de la construction mixte acier-béton. La connexion entre une partie en acier (un profilé, un bac collaborant, etc.), et une autre en béton permet d’obtenir un fonctionnement en commun des deux matériaux. Chacun est sollicité dans son domaine de prédilection : la traction pour l’acier et la compression pour le béton.

État de contrainte dans l’âme et effort de glissement

La Figure 2 montre l’état de contrainte en plusieurs points de l’âme d’une tranche d’un profilé reconstitué soudé, sollicité par un moment de flexion M (qui varie le long de la poutre) et un effort tranchant V. La contrainte est, par définition, un effort divisé par une surface. On ne peut pas définir un état de contrainte strictement en un point, car la surface serait alors nulle et on trouverait une contrainte infinie. Un état de contrainte « en un point » est en fait une représentation théorique consistant à isoler une petite portion de matière entourant le point. Les effets du reste de la matière sur les bords de cet élément isolé sont alors représentés sous forme de contraintes normales ou tangentielles.

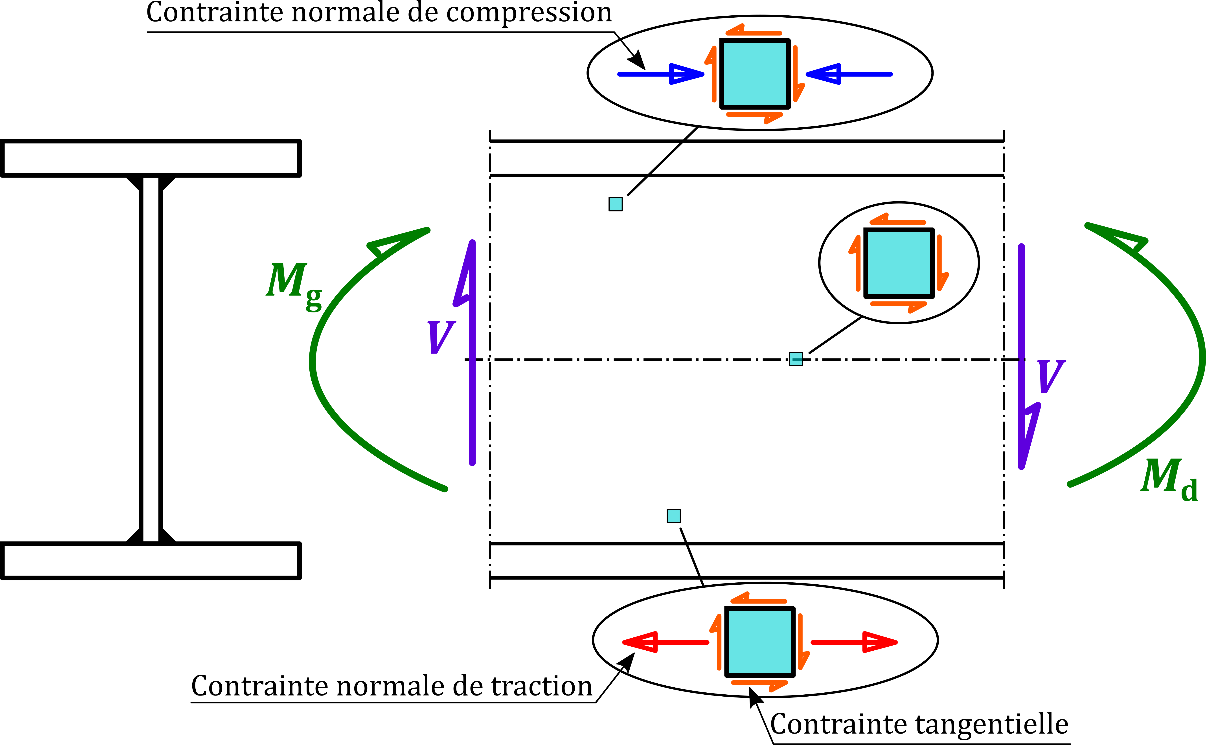
Les contraintes tangentielles « en un point » sont toutes égales, en valeur absolue, qu’elles soient appliquées sur une facette « verticale » ou sur une facette « horizontale ». Cette égalité est nécessaire pour assurer l’équilibre de la portion de matière isolée.

La contrainte tangentielle 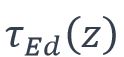 à la hauteur  de la section peut être déterminée, dans le cadre d’un comportement élastique du matériau, à partir de l’effort tranchant V_Ed , sollicitant la section en utilisant l’expression suivante, voir la Figure 3 :

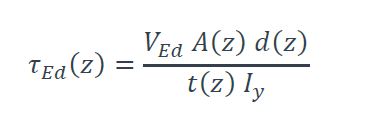
Avec :

V_Ed       Effort tranchant sollicitant la section.

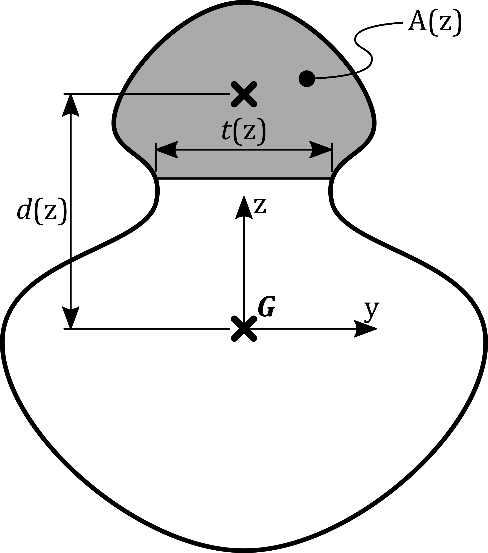
A_(z)      Aire de la portion de la section située entre la hauteur z et la fibre extrême la plus proche.

d_(z)       Distance entre le centre de gravité de la section complète et celui de la portion de la section située entre la hauteur z  et la fibre extrême la plus proche.

 t _(z)     Épaisseur de la section à la hauteur z .

I_y          Inertie de flexion de la section complète.

Cette contrainte tangentielle 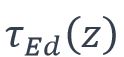 correspond à la contrainte de glissement longitudinal. En multipliant cette contrainte par l’épaisseur t _(z)  on obtient l’effort par unité de longueur, noté ici g_Ed(z), de glissement longitudinal à la hauteur  de la section :

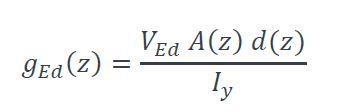
Cas de la jonction âme semelle pour une section en I

En considérant pour z la hauteur correspondant à la transition âme-semelle, on obtient l’effort de glissement à transmettre entre cette semelle et l’âme (voir la Figure 4) :

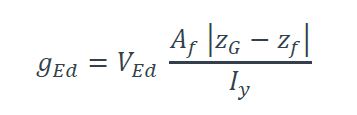
Avec :

 A_f        Aire de la semelle considérée.

Z_G       Hauteur du centre de gravité de la section complète ( Z_G=0 si l’origine du repère correspond au centre de gravité de la section).

Z_f        Hauteur du centre de gravité de la semelle considérée.

Figure 4 : Notation pour le calcul de l’effort de glissement dans les soudures âme-semelles d’un PRS

Note : L’effort de glissement longitudinal équilibre la différence d’effort normal dans la semelle entre deux sections proches. En effet, l’effort normal dans la semelle varient le long de celle-ci du fait de la variation du moment de flexion. Et la variation (c’est à dire la dérivée) du moment de flexion le long de la barre correspond mathématiquement à l’effort tranchant. Cela permet évidement de retrouver l’expression ci-dessus.

Référence

• [1]    NF EN 1993-1-8 : Eurocode 3 – Calcul des structures en acier – Partie 1-8 : calcul des assemblages. AFNOR, 2005.

Télécharger le document

Antony Rodier, chef du service formation, CTICM