Choix du matériau acier vis-à-vis de la rupture fragile – 3e partie

Cet article en trois parties explique la prise en compte de la rupture fragile selon la norme NF EN 1993-1-10 et selon le rapport JRC-CECM EUR 23510 servant de son document d’information.

Cette partie présente de manière synthétique les règles pour le choix des aciers vis-à-vis de la rupture fragile selon le rapport EUR 23510.

Introduction

Dans la 1^re partie de cet article, il a été montré que le but de la méthodologie générale proposée dans la norme NF EN 1993-1-10 et détaillée dans le rapport JRC-CECM de Sedlacek et al (EUR 23510) est de se prononcer sur l’adéquation du choix de la qualité d’un acier donné, vis-à-vis de sa ductilité, par une des deux approches.

La seconde des deux approches, limitée à un nombre de situations plutôt rarement rencontrées, est détaillée dans cette 3^e partie de ce texte. Pour rappel, la première approche, couvrant la plupart des situations rencontrées dans la pratique, est détaillée dans sa 2^e partie.

Approche 2 – Justification par les calculs

Généralités

Lorsque l’une ou plusieurs des conditions d’utilisation du Tableau 2.1 de la NF EN 1993-1-10 (voir la 2^e partie de cet article) ne sont pas rencontrées, la NF EN 1993-1-10, paragraphe 2.2(3), offre la possibilité de réaliser des calculs afin de s’assurer que, pour un acier spécifié et un taux de travail donné :

• soit la taille d’un défaut est inférieure à la taille de défaut critique pour une température de référence ;
• soit la température de référence au site potentiel de rupture est supérieure à la température provoquant des ruptures fragiles.

Les sites potentiels de rupture sont, a priori, les zones où les contraintes de traction sont les plus élevées, compte tenu des concentrations de contraintes.

Note : les effets des concentrations de contrainte peuvent être soit extraits de la littérature spécialisée existante, soit calculés par éléments finis.

La NF EN 1993-1-10 ne donne qu’une description très générale de la méthodologie. Il n’y a aucune référence à un document quelconque permettant de réaliser une justification par calculs. Pourtant, la méthodologie générale détaillée est donnée dans le rapport JRC-CECM EUR 23510.

Elle consiste à comparer l’effet des actions à la résistance, en utilisant comme fonction d’état :

• Soit le coefficient d’intensité de contrainte (K_appl,d, fonction de la contrainte de référence et de la taille de défaut), où la résistance est donnée par le paramètre K_mat,d, ténacité à la rupture du matériau à la température basse de service ;

Note : le coefficient d’intensité de contrainte ne doit pas être confondu avec la notion de concentration de contrainte ; il est exprimé plus loin dans cette partie.

• Soit la température de référence T_Ed, où la résistance est donnée par une température normalisée, fonction de la température de transition caractérisant la résilience de l’acier (T_27J pour les nuances d’acier les plus utilisées).

Note : la ténacité à la rupture et la résilience a été abordée dans la 1^re partie de ce texte.

Pour les aciers de construction (tôles et profilés laminés), vu le faible coût et le caractère répandu des essais de résilience, c’est la seconde approche qui est préférée. (Elle est formalisée dans les textes mentionnés, NF EN 1993-1-10 et le rapport JRC-CECM EUR 23510, par le biais d’une corrélation admise entre la ténacité et la résilience, bien validée pour les aciers de construction.)

Note : pour d’autres aciers (aciers moulés, par exemple), il est nécessaire de procéder à la détermination de leur ténacité à la rupture par essais et à une comparaison entre le coefficient d’intensité de contrainte et la ténacité à la rupture exclusivement.

Les autres paramètres pris en compte sont :

• la géométrie des détails constructifs,
• l’état de contraintes, y compris les concentrations de contraintes dues à la géométrie,
• les vitesses de mise en charge,
• le niveau des contraintes résiduelles,
• les défauts susceptibles d’être présents dans les pièces,
• le chargement de fatigue (variation de contrainte due au trafic).

Philosophie de calcul

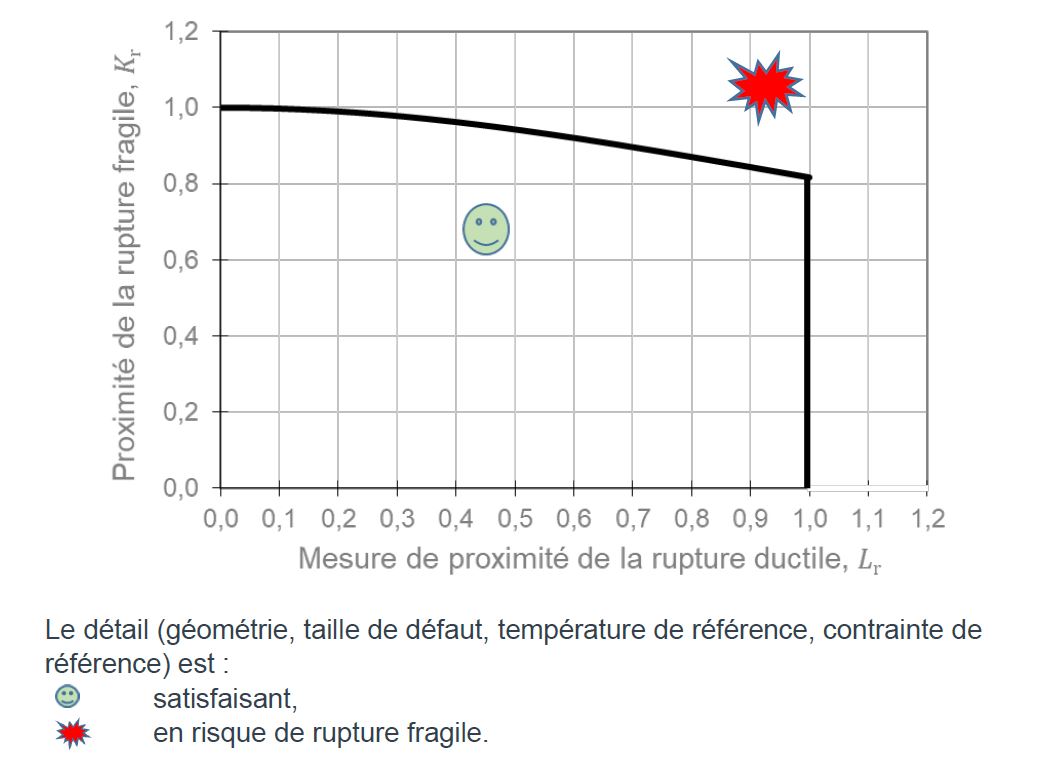
La méthode R6, mentionnée dans la 1^re partie de cet article, consiste à comparer les valeurs des deux critères, K_r et L_r, qui ne sont pas détaillés dans ce texte, avec une courbe d’état limite présentée à la Figure 1. Si le calcul place le point (K_r,L_r) au-dessous de la courbe d’état limite, le détail constructif traité est satisfaisant. Si le point est au-dessus de la courbe, le détail n’est pas satisfaisant et il ne convient pas pour la température basse de service, combinée avec l’état de contraintes et les défauts susceptibles d’y être présents.

Note : on peut trouver plus d’informations sur les critères K_r et L_r dans le rapport JRC-CECM EUR 23510.

Comme déjà annoncé dans la 1^re partie de cet article, c’est la méthode R6 qui se trouve à l’origine des deux fonctions d’état déjà mentionnées plus haut :

• Celle basée sur la ténacité à la rupture du matériau à la température basse de service, et
• Celle basée sur la résilience Charpy.

Les deux fonctions d’état sont détaillées ci-dessous.

Calcul utilisant la ténacité à la rupture

Dans cette approche, il convient de considérer que la ductilité d’un détail constructif soumis à une contrainte de traction de calcul est suffisante si :

K_appl,d ≤ K_mat,d

où :

K_appl,d       est le coefficient d’intensité de contrainte, en [MPa√m], déterminé à l’aide de l’équation :

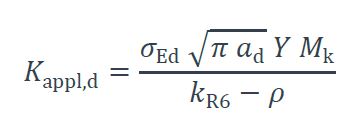
avec :

σ_Ed :     contrainte de référence, dont la détermination a été vue dans la 2^e partie de ce texte, en [MPa],

a_d :       taille de défaut critique, en [m], abordée plus loin,

Y M_k :   fonction de forme, avec :

Y(a_d) :   fonction de correction pour les différentes positions et formes de défauts, adimensionnelle,

M_k(a_d) : fonction de correction pour les différents types de détails constructifs, adimensionnelle,

k_R6 :      terme de correction pour prendre en compte l’erreur résultant de la non prise en compte de la plasticité locale au fond de défaut, adimensionnel,

ρ :        coefficient correcteur de plasticité pour les contraintes secondaires, adimensionnel ;

Note : les paramètres Y, M_k, k_R6 et ρ sont détaillés dans le rapport JRC-CECM EUR 23510.

K_mat,d       est la ténacité à la rupture du matériau à la température basse de service, en [MPa√m].

Calcul utilisant la résilience

Dans cette approche, il convient de considérer que la ductilité d’un élément de structure soumis à une contrainte de traction de calcul est suffisante si :

T_Ed ≥ T_Rd

où :

T_Ed :        est la température de référence au site potentiel de rupture exprimée comme suit :

T_Ed = T_md + ΔT_r +ΔT_s + ΔT_R + ΔT_e +ΔT_e,cf

avec :

T_md :     température minimale de service, vue dans la 2^e partie de ce texte,

ΔT_r :     terme de correction pour les pertes de rayonnement, également vu dans la 2^e partie de ce texte,

ΔT_σ :     décalage induit par la contrainte, la limite d’élasticité, l’imperfection de type fissure et la forme et les dimensions du détail constructif, exprimé par la formule :

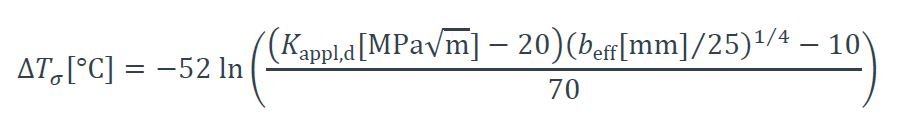
où b_eff est la longueur critique du défaut, fonction des différentes positions et formes de défauts, donnée dans le rapport JRC-CECM EUR 23510,

ΔT_R :    terme de sécurité, pour différencier le niveau de fiabilité, donné dans le rapport JRC-CECM EUR 23510 ; dans le cas de l’utilisation des valeurs de résilience en provenance des normes de produits : ΔT_R = +7°C,

ΔT_έ:     terme de correction pour la vitesse de déformation, vue dans la 2^e partie de ce texte,

ΔT_ε,cf – terme de correction pour le formage à froid, vue aussi dans la 2^e partie de ce texte ;

T_Rd :     est la température à laquelle on peut escompter un niveau adéquat de ténacité à la rupture dans les conditions examinées ; elle est déterminée à l’aide de l’équation :

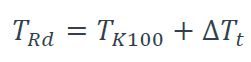
avec :

T_K100 :   température à laquelle le matériau possède une ténacité à la rupture K_mat,d de 100 MPa√m : T₁₀₀ = T_27J – 18,

ΔT_t :     terme de correction pour considérer la variation de la ténacité de du matériau dans le sens de l’épaisseur.

Note : ce dernier terme est donné dans le détail dans le rapport JRC-CECM EUR 23510.

Taille de défaut critique

La détermination de la taille de défaut critique a_d est le passage obligatoire pour effectuer les deux calculs donnés plus haut. De plus, il est possible de la comparer avec la taille d’un défaut présent dans un détail constructif, pour une contrainte de référence s_Ed et une température de référence T_Ed données : plus cette taille est grande, plus important sera le défaut acceptable, soit un défaut initial, soit une fissure de fatigue (fissure obtenue avec la propagation d’un défaut initial par les actions cycliques).

La Figure 2 montre les résultats de ces calculs sur l’exemple d’une paroi de l’épaisseur de 22 mm en acier S275. Ces calculs ont été réalisés en variant la température de référence T_Ed, la température de transition T_27J caractérisant la résilience (la qualité) de l’acier et en variant le rapport entre la contrainte de référence σ_Ed et la limite d’élasticité f_y (25 %, 50 % et 75 %).

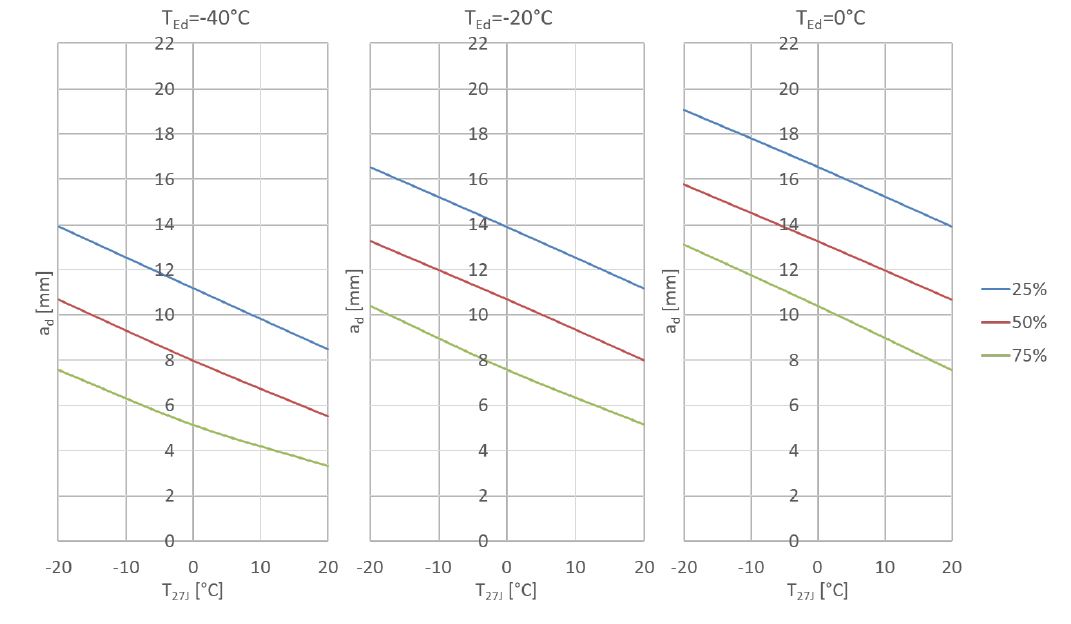
Note : Les résultats présentés à la Figure 2 ne sont aucunement d’une validité universelle. Il s’agit d’une configuration particulière, d’une forme et d’un emplacement de défaut précis.

Le Figure 2 montre que :

• plus élevée est la qualité d’acier (plus basse est la température de transition T_27J), plus grande est la taille de défaut critique ;
• plus élevée est la température de référence T_Ed, plus grande est la taille de défaut critique ;
• moins élevé est le taux de travail (σ_Ed/f_y), plus grande est la taille de défaut critique.

Cette taille varie au cours de la vie de l’ouvrage, car trois des paramètres dont elle dépend (niveau de contraintes, vitesse de chargement et température) changent en continu. Une représentation très schématique de ce phénomène est montrée à la Figure 3. Pour trouver la taille la plus défavorable, on se positionne généralement dans la situation la plus défavorable : le plus grand niveau de contraintes (et, à l’occurrence, la plus grande vitesse de chargement) censé pouvoir se produire simultanément avec la plus basse température de service.

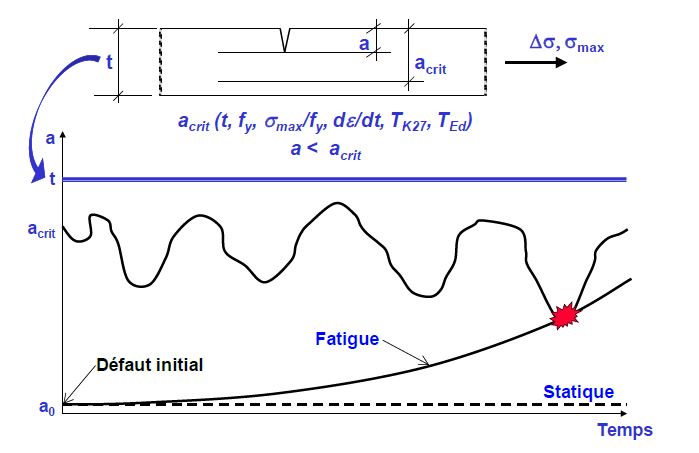
Ce calcul est formalisé et la taille de défaut critique est calculée à partir d’un des deux types de calcul (utilisant la ténacité à la rupture, ou utilisant la résilience) donnés ci-dessus.

Exemple numérique

Le calcul basé sur le rapport JRC-CECM EUR 23510 est complexe et dépasse le cadre de ce texte. Un exemple de calcul suivant cette méthodologie, intitulé « Calcul à la rupture fragile d’un détail constructif – Application au raboutage des semelles », a été rédigé par l’auteur de ce texte et publié dans la Revue construction métallique N°1-2009, téléchargeable ici.

Références

NF EN 1993-1-10 : Eurocode 3 – Calcul des structures en acier – Partie 1-10 : Choix des qualités d’acier ; AFNOR, 2005.

Sedlacek G. et al : Commentary and worked examples to EN 1993-1-10 “Material toughness and through thickness properties” and other toughness oriented rules in EN 1993 ; JRC-ECCS, EUR 23510 EN, 2008.

Lukić M. : Calcul à la rupture fragile d’un détail constructif – Application au raboutage des semelles ; Revue Construction métallique, N°1-2009.

Télécharger le texte

Mladen Lukić , directeur de projet de recherche, CTICM