Résistance plastique d’une section en I bissymétrique sous interaction de flexion, cisaillement et effort normal – Partie I : formulation analytique.
La résistance d’une section soumise à une combinaison de flexion, cisaillement et effort normal doit être vérifiée d’après les prescriptions du §6.2.10 de l’EN 1993-1-1 [1]. Les effets de l’effort normal et de l’effort tranchant doivent être pris en compte lors de la détermination du moment résistant en section. Aucune expression n’étant proposée dans l’EN 1993-1-1 [1] pour déterminer ce moment résistant, le présent article donne une méthode pour le calculer.
Domaine d’application
Cet article présente une méthode de calcul permettant d’obtenir le moment résistant plastique pour une section en I bissymétrique applicable en présence de :
- Un effort normal NEd ;
- Un moment de flexion dans le plan de forte inertie My,Ed ;
- Un effort tranchant parallèle à l’âme VEd.
Pour la méthode de calcul présentée dans cet article, les sollicitations doivent être prises en compte en valeur absolue.
Les expressions données ci-après ont été développées en considérant la section transversale d’un profilé reconstitué par soudage (PRS). Elles restent applicables dans les cas de profilés laminés en négligeant les congés de raccordement.
Les dimensions d’une section transversale en I doublement symétrique sont présentées à la Figure 1.
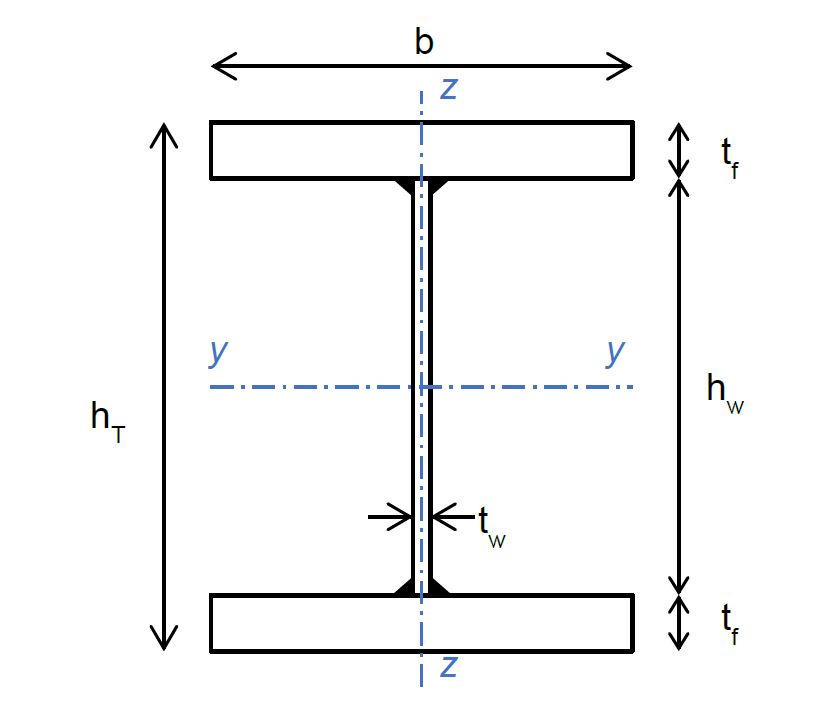
L’incidence de l’effort tranchant sur la résistance de la section est à examiner lorsque :
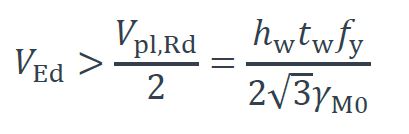
L’influence de l’effort tranchant est alors prise en compte dans le calcul du moment résistant en utilisant une limite d’élasticité réduite pour l’âme, conformément au §6.2.10 de l’EN 1993-1-1 [1] :
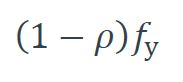
où fy est la limite d’élasticité de l’acier utilisé pour l’âme et les semelles et :
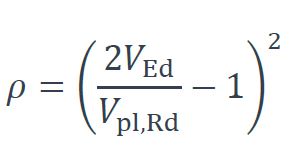
Conditions de résistance sous sollicitations simples
Préalablement au calcul de la résistance plastique de la section en tenant compte des sollicitations qui agissent simultanément dans une section, il convient de s’assurer que le critère de résistance pour chaque sollicitation est satisfait.
NOTE La résistance plastique de la section ne peut être mobilisée que si celle-ci est de Classe 1 ou 2 au sens de l’Eurocode 3 Partie 1-1 [1].
Conformément aux paragraphes 6.2.3 à 6.2.6 de l’EN 1993-1-1 [1], les conditions suivantes doivent être vérifiées :
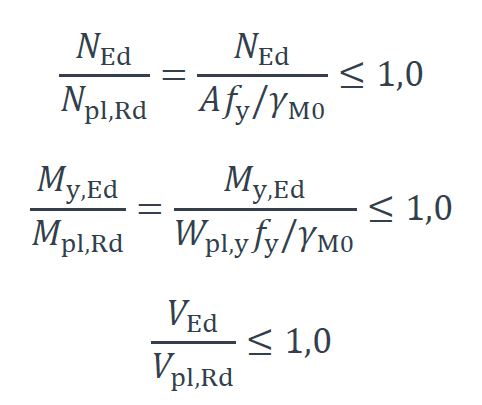
NOTE Le module de résistance plastique en flexion par rapport à l’axe y–y d’une section en I doublement symétrique est :
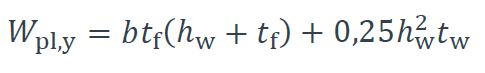
Position de l’axe neutre plastique
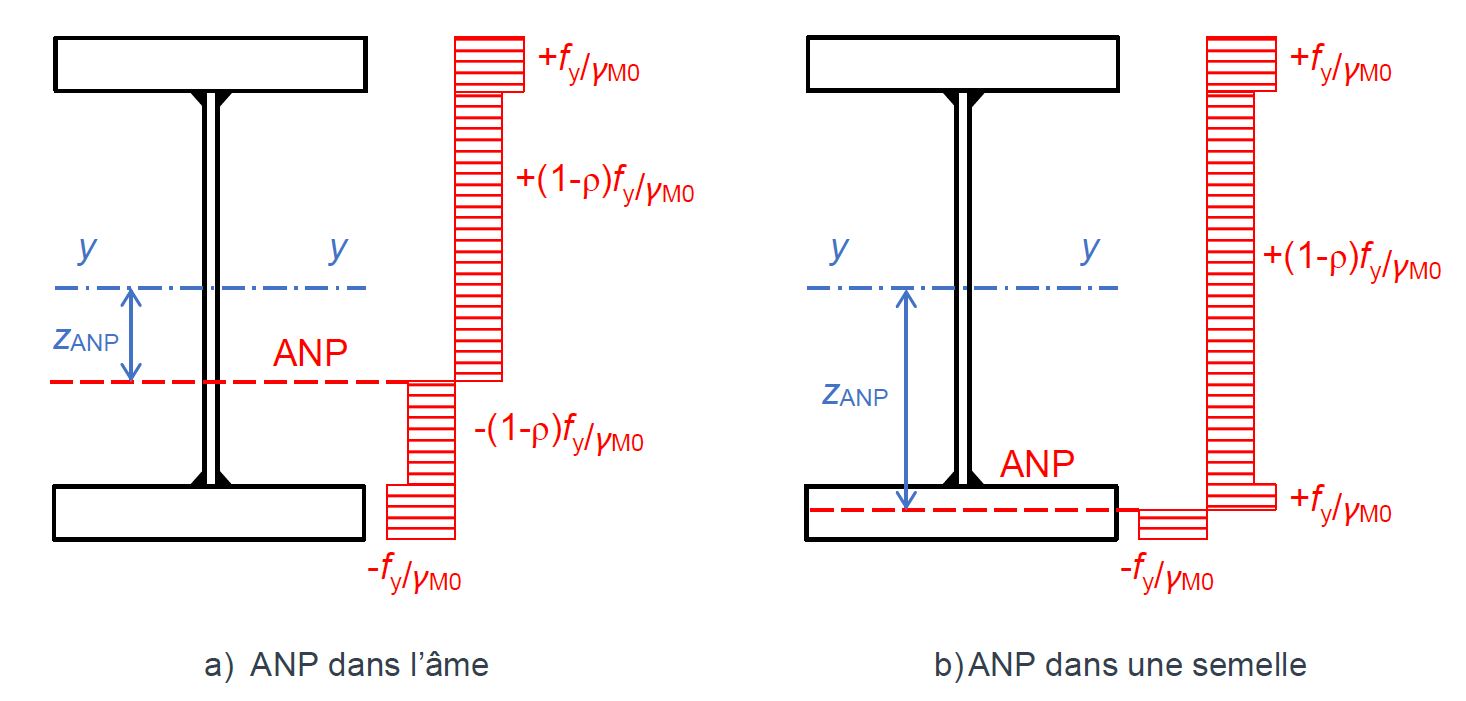
La Figure 2 présente la distribution plastique des contraintes normales lorsque l’axe neutre plastique (ANP) est situé dans l’âme (voir Figure 2a)) ou dans une semelle (voir Figure 2b)). Les contraintes de compression sont représentées avec un signe positif et les contraintes de traction avec un signe négatif, en homogénéité avec l’EN 1993-1-1 [1].
L’ANP se situe dans l’âme (voir Figure 2a)) si la condition suivante est respectée :
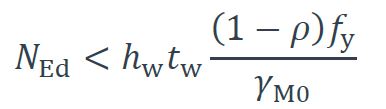
Dans le cas contraire, l’ANP se situe dans l’une des semelles (voir Figure 2b)).
La distance zANP entre le centre de gravité de la section et l’ANP lorsqu’il se situe dans l’âme (voir Figure 2a)) est :
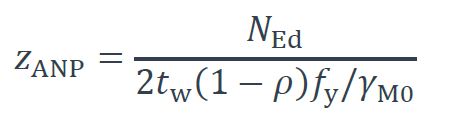
La distance zANP entre le centre de gravité de la section et l’ANP lorsqu’il se situe dans une semelle (voir Figure 2b)) est :
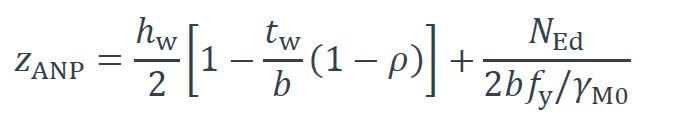
Moment résistant plastique lorsque l’ANP est dans l’âme
Dans le cas où l’ANP est situé dans l’âme, le moment résistant plastique MNV,y,Rd prenant en compte les effets de l’effort tranchant et de l’effort normal est :
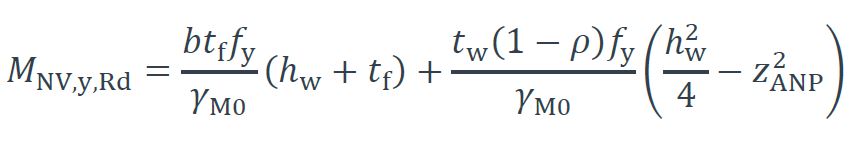
Moment résistant plastique lorsque l’ANP est dans une semelle
Si l’ANP est situé dans une semelle, le moment résistant plastique MNV,y,Rd prenant en compte les effets de l’effort tranchant et de l’effort normal est :
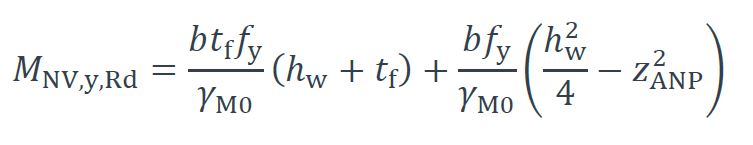
Références
[1] NF EN 1993-1-1 – Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR, octobre 2005
Maxime Lebastard, ingénieur de recherche – CTICM