Résistance de calcul à température élevée des éléments métalliques #3 – Poutres simplement fléchies de classe 1, 2 ou 3 sans déversement

La partie 1-2 de l’Eurocode 3 et son annexe nationale française [1, 2], dédiés aux éléments de structure métallique, fournit différentes formules permettant de calculer la résistance au feu des éléments de structure métallique, tels que tirants, poutres et poteaux. Ce texte est consacré au calcul de la résistance au feu des éléments tendus et des éléments axialement comprimés de classe 1, 2 ou 3 sans risque d’instabilité.

Cet article est le troisième d’une série de 7 consacrés à la résistance de calcul au feu :

1. Résistance de calcul à température élevée des éléments métalliques – Introduction
2. Résistance de calcul à température élevée des éléments métalliques – Éléments tendus ou axialement comprimés sans risque d’instabilité
3. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1, 2 ou 3 sans déversement
4. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1,2, 3 sujettes au déversement
5. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés axialement de classe 1, 2 et 3 sujets au flambement
6. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés et fléchis de classe 1, 2 ou 3
7. Résistance de calcul à température élevée des éléments métalliques – Assemblages

Moment résistant de calcul pour une section avec une distribution uniforme de température

Le moment résistant de calcul M_fi,θ,Rdd’une section transversale de classe 1, 2 ou 3 exposée sur 4 faces et présentant une température uniforme θ_a peut être calculée au moyen de l’expression suivante :

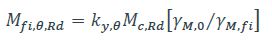
Où
M_c,Rd est le moment résistant (plastique ou élastique) de la section brute M_pl,Rd pour le calcul à température normale, selon l’EN 1993 1 1 [3], ou le moment résistant réduit pour le calcul à température normale, prenant en compte les effets du cisaillement si nécessaire, selon l’EN 1993 1 1 [3] ;
k_y,θ est le facteur de réduction pour la limite d’élasticité de l’acier à la température θ_a
γ_M,fi est le coefficient partiel de sécurité pour l’acier en situation d’incendie. Pour rappel, sa valeur est fixée à 1,0 dans l’annexe nationale française de l’EN 1993-1-2.

γ_(M,0) est le coefficient partiel pour la résistance des sections transversales à température normale;

Moment résistant de calcul pour une section avec une distribution non uniforme de température

Il est fréquent que l’échauffement au sein des éléments structuraux en acier ne soit pas uniforme, en particulier pour les poutres de plancher supportant une dalle en béton. Dans ce cas, le moment résistant de calcul M_fi,t,Rd au temps t d’une section de classe 1, 2 ou 3 peut être déterminé au moyen de l’expression :

Où
M_fi,θ,Rd est le moment résistant de calcul de la section transversale de la poutre avec une température uniforme θ_a atteinte au temps t dans une section transversale qui n’est pas thermiquement affectée par un appui ;
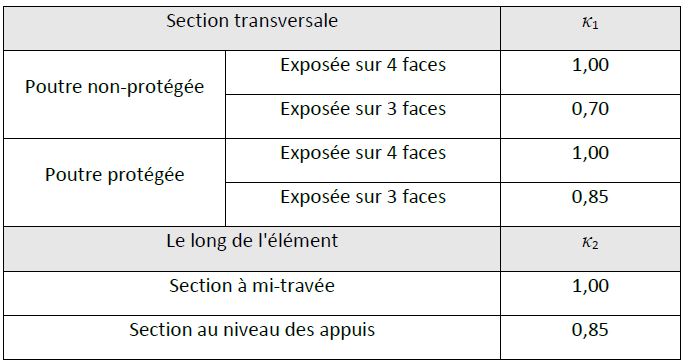
κ₁ et κ₂ sont des coefficients d’adaptation permettant de prendre en compte une distribution de température non uniforme en section et sur la longueur de la poutre (cf. tableau 1) ;

Réduction du moment résistant en présente d’un effort tranchant

En principe, la présence d’un effort tranchant peut conduire à une réduction du moment résistant. Toutefois, l’interaction entre moment résistant et effort tranchant reste assez limitée. En effet, elle n’est susceptible d’affecter le dimensionnement que dans un nombre restreint de situations, à savoir :

• Les poutres soumises à des forces concentrées très importantes près des appuis ;
• Les poutres continues pour lesquelles les appuis intérieurs sont soumis à la fois à des extrema d’effort tranchant et de moment fléchissant.

Selon la partie 1-2 de l’EN1993-1-2, lorsqu’en situation d’incendie la valeur de calcul de l’effort tranchant n’excède pas 50 % de la résistance au cisaillement, c’est-à-dire V_fi,Ed=0,5V_fi,t,Rd, l’effet de l’effort tranchant sur le moment résistant peut être négligé. Dans ce cas, le moment résistant de la section transversale à la flexion M_c,Rd peut être calculé directement à partir des relations suivantes :
Pour les éléments de classe 1 et 2 : M_c,Rd=W_plf_y
Pour les éléments de classe 3 : M_c,Rd=W_elf_y
Où :
W_pl est le module de flexion plastique de la section transversale par rapport à l’axe approprié ;
W_el est le module de flexion élastique de la section transversale par rapport à l’axe approprié ;
f_y est la valeur nominale de la limite d’élasticité de l’acier à température normale.
Lorsque V_fi,Ed excède 50% de V_fi,t,Rd, il faut tenir compte de l’effet de l’effort tranchant sur le moment résistant de la section transversale. Le principe consiste à calculer le moment résistant M_c,Rd en utilisant une limite d’élasticité réduite, de valeur (1-ρ)f_y , pour l’aire de cisaillement, avec :

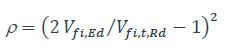
Dans le cas d’une section en I ou H doublement symétrique de classe 1 ou 2, le moment résistant réduit par l’effort tranchant à température normale peut être obtenu par :

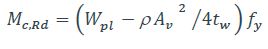
où t_w et A_v sont respectivement l’épaisseur de l’âme et l’aire de cisaillement du profilé métallique. Dans le cas d’une section en I ou H doublement symétrique de classe 3, le moment résistant réduit par l’effort tranchant à température normale peut être calculé de manière sécuritaire par :

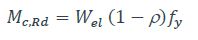
Rappelons que la présence d’un effort tranchant requiert également d’effectuer une vérification de la résistance au cisaillement de la section transversale de l’élément.

Résistance de calcul à l’effort tranchant

La résistance de calcul au cisaillement V_fi,t,Rd au temps t peut être calculée à partir de la relation suivante :

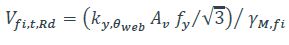
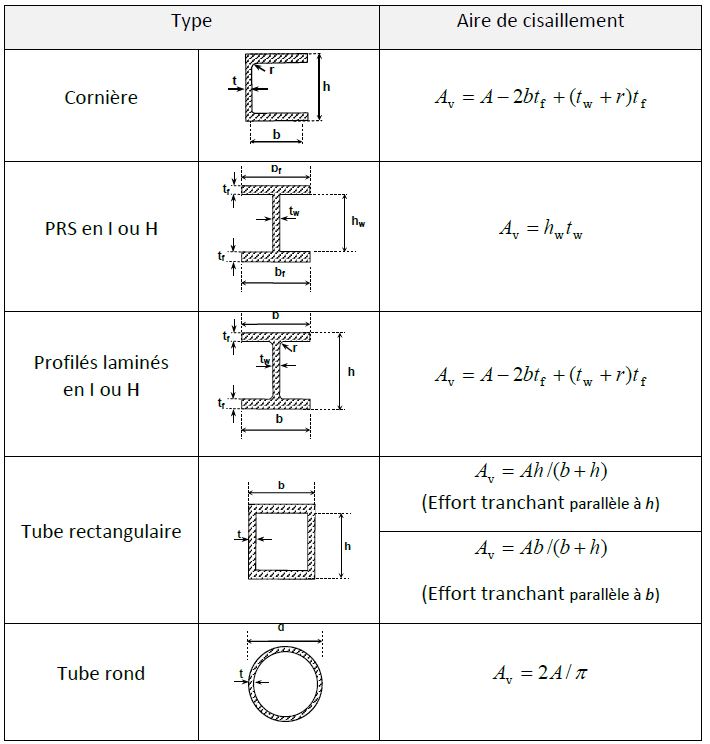
A_v est l’aire de cisaillement du profilé métallique. Elle peut être calculée à partir des relations données dans le tableau 2 ;
θ_web est la température moyenne dans l’âme de la section. Cette température peut être supposée, en se plaçant du côté de la sécurité, égale à la température uniforme θ_a ;

k_y,θweb est le facteur de réduction pour la limite d’élasticité de l’acier à la température θ_web ;

Références

[1] NF EN 1993-1-2 – Eurocode 3 – Calcul des structures en acier – Partie 1-2: Règles générales – Calcul du comportement au feu, avril 2005.
[2] NF EN 1993-1-2/NA – Eurocode 3 « Calcul des structures en acier » – Partie 1-2: Règles générales – Calcul du comportement au feu, annexe nationale à la NF EN 1993-1-2, octobre 2007.
[3] NF EN 1993-1-1 – Eurocode 3 – Calcul des structures en acier – Partie 1-1: Règles générales et règles pour les bâtiments, octobre 2005.

Télécharger le document

Christophe Renaud, directeur de projet de recherche – CTICM