Résistance de calcul à température élevée des éléments métalliques #5 –Éléments comprimés axialement de classe 1, 2 et 3 sujets au flambement

La partie 1-2 de l’Eurocode 3 et son annexe nationale française [1, 2], dédiés aux éléments de structure métallique, fournit différentes formules permettant de calculer la résistance au feu des éléments de structure métallique, tels que tirants, poutres et poteaux. L’article qui suit est consacré au calcul de la résistance au feu des éléments comprimés axialement, de classe 1, 2 ou 3 sujets au flambement.

Cet article est le cinquième d’une série de 7 consacrés à la résistance de calcul au feu :

1. Résistance de calcul à température élevée des éléments métalliques – Introduction
2. Résistance de calcul à température élevée des éléments métalliques – Éléments tendus ou axialement comprimés sans risque d’instabilité
3. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1, 2 ou 3 sans déversement
4. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1,2, 3 sujettes au déversement
5. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés axialement de classe 1, 2 et 3 sujets au flambement
6. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés et fléchis de classe 1, 2 ou 3
7. Résistance de calcul à température élevée des éléments métalliques – Assemblages

Calcul de la résistance au flambement à température élevée

Pour un élément comprimé axialement de classe 1, 2 ou 3, le calcul est similaire à celui présenté pour un élément tendu, excepté qu’il doit tenir compte du risque de flambement.

Selon l’EN 1993-1-2, la résistance de calcul au flambement N_b,fi,t,Rd au temps t d’un élément axialement comprimé de classe 1, 2 ou 3, dont la température θ est uniforme, peut être calculée avec la formule suivante :

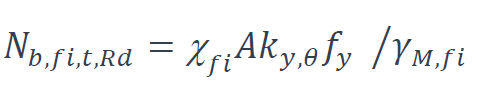
Où

χ_fi est le facteur de réduction pour le flambement par flexion en situation d’incendie. Il convient de prendre la plus petite valeur de χ_y,fi  et χ_z,fi ;

k_y,θ est le facteur de réduction de la limite d’élasticité de l’acier à la température θ ;

f_y est la valeur nominale de la limite d’élasticité de l’acier à température normale ; 

γ_M,fi est le coefficient partiel de sécurité pour l’acier en situation d’incendie. Pour rappel, sa valeur est fixée à 1,0 dans l’annexe nationale française de l’EN 1993-1-2 [2].

Lors d’un calcul reposant sur une exposition à l’incendie normalisé, il convient de signaler que la résistance de calcul N_b,fi,t,Rd  au temps t d’un élément axialement comprimé présentant une distribution non uniforme de sa température peut être prise égale à la résistance de calcul N_b,fi,θ,Rd d’un élément comprimé présentant une température uniforme θ_α  égale à la température maximale θ_α,max  atteinte au temps t.

Calcul du facteur de réduction pour le flambement à température élevée

Le facteur de réduction pour le flambement peut être calculé à partir de la formule suivante :

L’élancement réduit 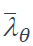 pour la température θ  est donné par l’expression :

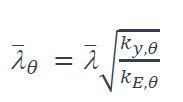
Où

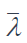 est l’élancement pour le flambement par flexion considéré ;

k_y,θ est le facteur de réduction de la limite d’élasticité de l’acier à la température θ  ;

k_E,θ est le facteur de réduction pour le module d’élasticité de l’acier à la température θ .

Calcul de l’élancement réduit pour le flambement par flexion

Pour le flambement par flexion, l’élancement réduit d’un élément de classe 1, 2 ou 3 à température normale peut être calculé selon l’EN 1993-1-1 [3] à partir de la relation suivante :

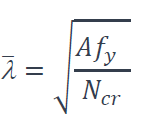
Où

 A est l’aire de la section transversale brute ;

N_cr est la force critique élastique pour le mode de flambement considéré basée sur les propriétés de la section transversale brute, en utilisant la longueur de flambement en situation d’incendie l_fi .

En alternative, l’élancement réduit pour le flambement par flexion peut également être calculé à partir de la formule suivante :

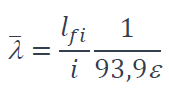
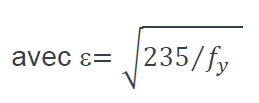
où  i est le rayon de giration par rapport à l’axe de flexion approprié et l_fi  est la longueur du flambement en situation d’incendie.

Détermination de la longueur de flambement en situation d’incendie

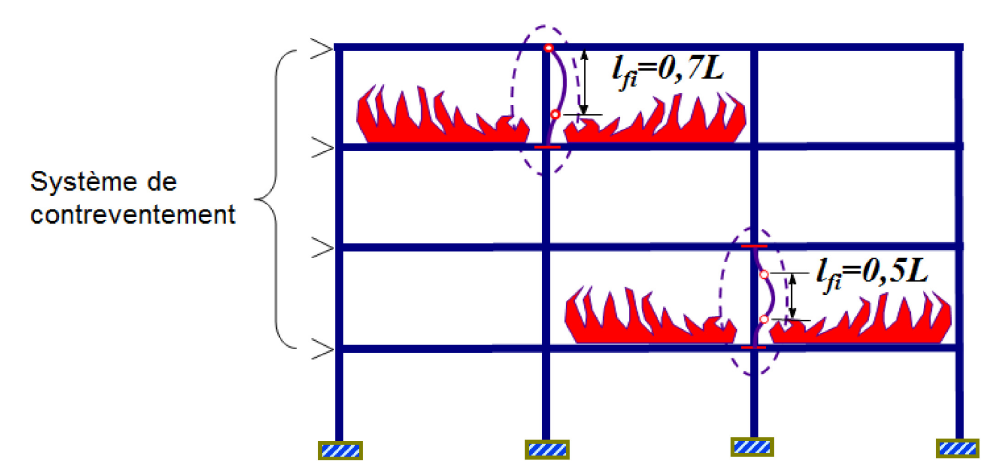
Pour les poteaux, la longueur de flambement en situation d’incendie peut être différente de la valeur utilisée pour le dimensionnement à froid. En effet, dans une ossature stabilisée par des contreventements ou des parois rigides, la longueur de flambement l_fi  d’un poteau d’étage peut être déterminée habituellement en le considérant comme encastré à ses extrémités, à condition que le degré de résistance au feu des éléments de construction qui séparent ces étages soit au moins égal à celui du poteau.

À partir de ce principe, dans le cas d’une ossature contreventée, la longueur de flambement l_fi est égale à 0,5×L pour un étage intermédiaire et à 0,7×L au dernier étage, L étant la longueur d’épure de l’étage considéré (voir Figure 6‑3). Pour le premier étage, la longueur de flambement est 0,5×L si le pied de poteau est encastré à sa base par des dispositions constructives, sinon elle est égale à 0,7×L.

Références

[1] NF EN 1993-1-2 – Eurocode 3 – Calcul des structures en acier – Partie 1-2: Règles générales – Calcul du comportement au feu, avril 2005.

[2] NF EN 1993-1-2/NA – Eurocode 3 « Calcul des structures en acier » – Partie 1-2: Règles générales – Calcul du comportement au feu, annexe nationale à la NF EN 1993-1-2, octobre 2007.

[3] NF EN 1993-1-1 – Eurocode 3 – Calcul des structures en acier – Partie 1-1: Règles générales et règles pour les bâtiments, octobre 2005.

Télécharger le document

Christophe Renaud, directeur de projet de recherche – CTICM