Méthode simplifiée de calcul de la résistance d’une section de classe 4
Selon l’Eurocode 3 Partie 1-1, pour une section de classe 4, il est possible de redéfinir la classe d’une section en se référant à la valeur réelle de la contrainte maximale de compression au lieu de se référer à la limite d’élasticité. Lorsqu’elle est applicable, cette méthode permet d’éviter de calculer les caractéristiques efficaces de la section, en ayant ainsi la possibilité de justifier sa résistance comme une section de classe 3.
Principe de la méthode
Conformément à l’Eurocode 3 Partie 1-1 [1], la classe d’une section est déterminée en supposant l’atteinte de sa résistance élastique ou plastique, en fonction du paramètre qui dépend de la limite d’élasticité fy de l’acier :
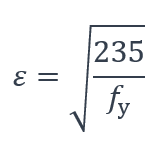
Il arrive toutefois que le dimensionnement d’un élément de structure soit gouverné par un autre état limite (par exemple l’état limite de service). Dans ce cas, une réserve de résistance est disponible à l’état limite ultime, et la contrainte dans la section est nettement inférieure à la limite d’élasticité. Pour une section considérée initialement comme étant de classe 4, il est possible, conformément à l’article 5.5.2 (9) de la norme, de reclasser la section en se référant à la contrainte normale maximale dans la paroi, c’est-à-dire en multipliant le paramètre par :
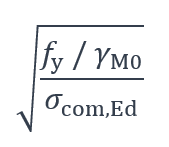
Où est la contrainte de compression maximale dans la paroi, sous l’effet d’une combinaison d’état limite ultime, déterminée à partir des caractéristiques de la section brute dont on veut déterminer la classe.
Soit :
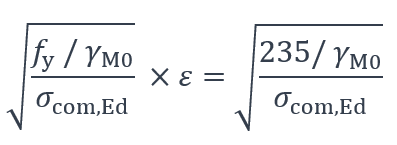
Condition d’application
Conformément à l’article 5.5.2(10) de la norme, cette méthode n’est applicable que s’il n’y a pas lieu de vérifier la barre par l’utilisation des formules de vérification vis-à-vis du flambement et/ou du déversement données en 6.3 de l’Eurocode 3 Partie 1-1. Voici deux exemples qui peuvent correspondre à cette situation :
- La barre ne présente aucun risque d’instabilité par flambement et/ou par déversement ;
- Les efforts dans la barre ont été calculés en tenant compte des imperfections locales et des effets du second ordre dans cette barre, de telle sorte qu’il n’y a plus lieu d’appliquer les formules habituelles de vérification de la barre vis-à-vis du flambement et/ou du déversement.
Exemple de calcul
Considérons une poutre de portée L = 12 m reposant sur deux appuis simples. La poutre est maintenue latéralement sur toute sa longueur au niveau de la semelle comprimée de sorte qu’elle ne présente aucun risque de déversement.
Cet exemple présente les vérifications vis-à-vis des états limites ultimes (ELU) et une vérification vis-à-vis des états limites de service (ELS). Pour la combinaison ELS, la flèche est limitée à L/500.
Géométrie et caractéristiques de la section transversale en I :

Moment de flexion maximal dans la poutre :
Combinaison ELU : 1,35 G + 1,5 Q = 31,83 kN/m
Le moment de flexion maximal est obtenu à mi-portée :
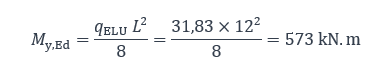
Classe de la section
Pour déterminer la classe de la section, par simplification, les cordons de soudure âme-semelle sont ignorés.
Classe de la semelle comprimée (NF EN 1993-1-1, Tableau 5.2 (feuille 2 sur 3)) :
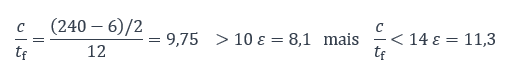
La semelle comprimée est de classe 3.
Classe de l’âme (NF EN 1993-1-1, Tableau 5.2 (feuille 1 sur 3)) :

L’âme est de classe 4.
En supposant qu’elle puisse atteindre sa pleine résistance, la section doit être considérée de classe 4.
Vérification de la résistance en flexion (ELU)
La section est de classe 4 mais elle est relativement peu sollicitée en flexion. En effet, la contrainte de compression maximale dans l’âme peut être calculée :
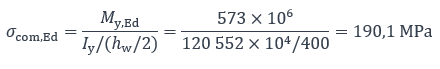
Il est possible de déterminer à nouveau la classe de l’âme en se référant à la contrainte de compression maximale, comme indiqué à l’article 5.5.2(9) de la norme NF EN 1993-1-1.
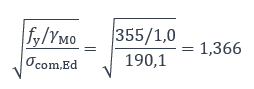
La limite d’élancement de l’âme pour la classe 3 est alors : 124×0,81×1,366 = 137,2
On constate que :
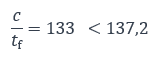
L’âme peut donc être reclassée en classe 3 et la section est alors de classe 3.
Compte tenu du niveau de contrainte normale dans l’âme, la résistance élastique en flexion est aisément vérifiée conformément à la NF EN 1993-1-1, 6.2.5 :
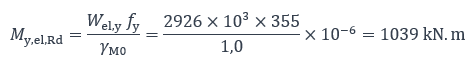
Et :
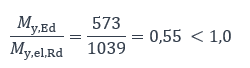
Vérification vis-à-vis des états limites de service (ELS)
Combinaison ELS : G + Q = 22 kN/m
La flèche maximale est calculée par :
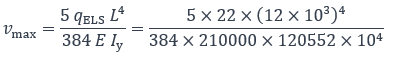
On obtient :

Conclusion
Pour l’exemple présenté ci-dessus, la poutre est dimensionnée pour la condition de flèche vis-à-vis des états limites de service. De ce fait, la poutre est relativement peu sollicitée vis-à-vis de l’état limite ultime de résistance en flexion. Il est alors possible de traiter l’âme, initialement considérée de classe 4, comme une âme de classe 3, ce qui permet de ne pas avoir à calculer les caractéristiques efficaces.
Référence
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
Alain Bureau, chef du service recherche construction métallique, CTICM