Utilisation du logiciel LTBeamN avec l’Eurocode 3 Partie 1-1
Cet article fournit des explications sur l’utilisation du logiciel LTBeamN dans le cadre de l’application des formules de vérification de résistance des barres au flambement et/ou au déversement selon l’Eurocode 3 Partie 1-1.
Introduction
Le logiciel LTBeamN [1] permet de calculer le mode propre d’instabilité élastique d’une barre comprimée et fléchie par rapport à l’axe de forte inertie de la section, pour l’instabilité hors plan de flexion (flambement hors plan et/ou déversement).
À partir de la version 2.0, il présente deux modes de fonctionnement, qu’il est possible de choisir dans les options de configuration du logiciel :
- Le mode simplifié permet de calculer le moment critique de déversement élastique d’une barre droite à section constante, simplement fléchie par rapport à l’axe de forte inertie de sa section transversale. Il correspond précisément au domaine d’utilisation de l’ancien logiciel LTBeam ;
- Le mode avancé permet de calculer un coefficient d’amplification critique d’une barre droite à section constante ou de géométrie linéairement variable, sollicitée en flexion par rapport à l’axe de forte inertie de sa section transversale et, le cas échéant, par un effort axial.
L’objet de cet article est d’apporter un éclairage sur l’utilisation des résultats du logiciel LTBeamN pour l’application des règles de l’Eurocode 3 Partie 1-1 [2].
Pour toute information sur le fonctionnement de LTBeamN, il est important de se reporter à l’aide accessible à partir du logiciel.
Note 1 : le logiciel LTBeam est définitivement remplacé par LTBeamN depuis septembre 2023.
Note 2 : il convient de noter que le résultat peut être fortement influencé par les conditions aux limites qui doivent refléter le comportement attendu de la barre étudiée.
Utilisation en « mode simplifié »
En mode simplifié, le logiciel LTBeamN calcule le mode propre d’instabilité élastique par déversement d’une barre à section constante, sollicitée en flexion par rapport à l’axe de forte inertie de sa section transversale. A ce mode propre, correspond un coefficient d’amplification critique, noté μcr dans le logiciel, qui est le coefficient par lequel il faudrait multiplier le chargement appliqué à la barre pour obtenir l’instabilité élastique au sens de la théorie eulérienne. Ensuite, le moment critique de déversement élastique, Mcr , est calculé comme le produit de ce coefficient par le moment de flexion maximal, MEd,max , sur la longueur totale de la barre :
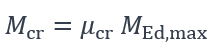
Ce moment critique de déversement élastique peut être utilisé pour effectuer la vérification de résistance au déversement d’une poutre, en appliquant le paragraphe 6.3.2 de l’Eurocode 3 Partie 1-1 [2].
Le paragraphe 6.3.3 de cette norme permet de vérifier la résistance vis-à-vis du flambement et du déversement d’une barre comprimée et fléchie, en utilisant notamment le coefficient de réduction calculé selon le paragraphe 6.3.2.
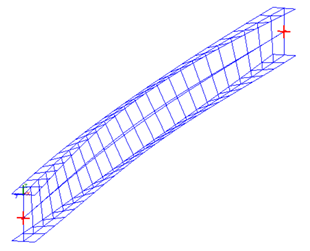
À titre d’exemple, la Figure 1 montre le mode propre de déversement élastique d’une poutre IPE 300 de longueur L = 6 m, avec des conditions d’appui à fourche aux extrémités, soumise à une charge gravitaire uniformément répartie sur la semelle supérieure.
Utilisation en « mode avancé »
En mode avancé, le logiciel LTBeamN permet de calculer le mode propre d’instabilité élastique d’une barre à section constante ou variable, sollicitée en flexion par rapport à l’axe de forte inertie de sa section transversale et/ou par un effort axial. Il s’agit exclusivement d’une instabilité hors plan de flexion.
Dans ce mode d’utilisation, il est permis de calculer un ou plusieurs modes propres d’instabilité élastique. D’un point de vue pratique, on retiendra le premier mode qui correspond au coefficient d’amplification critique le plus faible.
Lorsque la barre est sollicitée en flexion et/ou par un effort axial, le mode propre d’instabilité élastique est obtenu pour un chargement où les deux sollicitations sont multipliées par le même coefficient d’amplification critique, noté . Dans ce cas, ce coefficient peut être utilisé pour appliquer la « Méthode générale » du paragraphe 6.3.4 dans laquelle il correspond précisément au coefficient αcr,op :
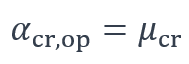
La méthode générale est particulièrement adaptée aux cas des barres à section variable, sollicitées par de la flexion dans le plan principal de forte inertie, et éventuellement par un effort axial. Le lecteur intéressé peut se reporter à la référence [3] qui donne un exemple d’application.
Pour l’application de cette méthode générale du paragraphe 6.3.4, le coefficient d’amplification critique doit être calculé en considérant que l’effort axial et le moment de flexion sont amplifiés simultanément, ce qui est le cas par défaut dans le logiciel LTBeamN.
Il y a lieu de préciser que, de manière générale, ce coefficient ne peut pas être utilisé pour l’application des méthodes des paragraphes 6.3.2 et 6.3.3. Cependant, dans le cas particulier où il s’agit d’une barre à section constante sollicitée uniquement en flexion, on retrouve bien sûr le même résultat qu’en « mode simplifié ».
À titre d’exemple, la Figure 2 montre le mode propre de déversement élastique d’une poutre PRS de longueur L = 6 m, constituée de semelles 240×12 mm et d’une âme de 6 mm de hauteur variant de 300 mm à 600 mm, avec des conditions d’appui à fourche aux extrémités. La poutre est soumise à un moment de 200 kN.m par rapport à l’axe de forte inertie de la section transversale, appliqué à l’extrémité de plus grande hauteur.
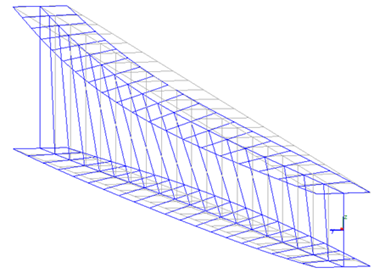
d’une poutre PRS à hauteur d’âme variable – mcr = 4,138
Synthèse
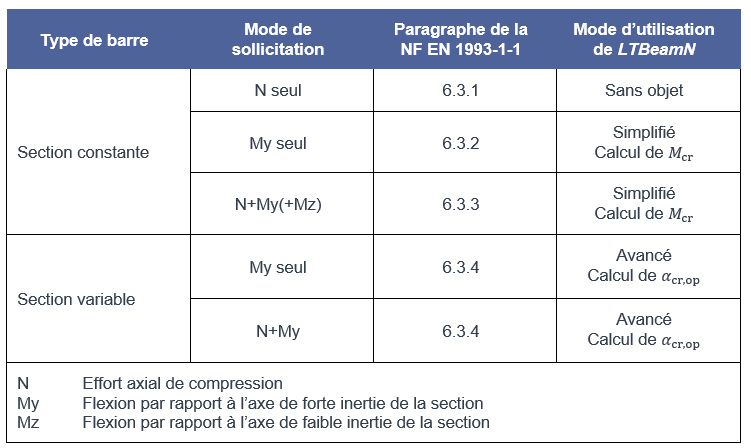
Le tableau suivant présente un aperçu des paragraphes de l’Eurocode 3 Partie 1-1 qu’il convient d’appliquer en fonction du type de barre et du mode de sollicitation pour les cas les plus fréquemment rencontrés en pratique.
Références
[1] Logiciel LTBeamN, version 2.0.1, instabilité élastique des poutres fléchies comprimées. Septembre 2023. Cticm. Disponible en téléchargement gratuit à partir du lien https://www.cticm.com/logiciel/ltbeamn/
[2] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[3] Beyer, A., Vérification de la stabilité d’un poteau à inertie variable selon l’Eurocode 3 Partie 1-1. Revue construction métallique n°1-2014. CTICM.
Alain Bureau, chef du service recherche construction métallique, CTICM