Résistance élastique en flexion positive des sections mixtes #2
La résistance élastique est un élément fondamental dans le contexte des poutres mixtes. Elle se réfère à la capacité de la poutre mixte, composée d’une poutre en acier et d’une dalle en béton, à subir des déformations temporaires réversibles sans subir de rupture, notamment lors de la flexion.
Introduction
Les développements présentés dans cet article sont principalement axés sur les sections de classe 3.
Cet article se concentre sur la présentation des différentes formules permettant de déterminer la résistance élastique des poutres mixtes en flexion, conformément aux normes en vigueur. L’objectif est de faciliter la compréhension et l’application des calculs essentiels pour une conception précise des poutres mixtes.
Le calcul de la résistance élastique des poutres mixtes est associé à la position de l’axe neutre élastique. L’axe neutre élastique est l’axe qui répartit les contraintes de manière à maintenir les déformations réversibles sous l’effet de la flexion.
Dans le contexte des normes en vigueur, il convient de noter que seule la section des poutres métalliques est classée en section, classe 1, 2, 3, ou 4 en fonction de leur voilement local. Les sections de classe 1 ou 2 peuvent être justifiées en plasticité ou en élasticité. Les sections de classe 3 sont justifiées en élasticité, mais peuvent éventuellement être reclassées en classe 2 efficace et justifiées en plasticité. Les sections de classe 4 sont également justifiées en élasticité, mais avec un calcul effectué sur une section efficace réduite pour prendre en compte le risque de voilement.
Hypothèse de résistance élastique
L’étude en flexion élastique est basée sur les hypothèses suivantes :
- L’hypothèse Navier-Bernoulli est valable pour la section mixte, toute section droite de poutre est supposée demeurer plane après déformation,
- La résistance en traction du béton est négligée,
- Les matériaux acier et béton ont un comportement élastique linéaire,
- Il convient de calculer les contraintes par la théorie élastique, en utilisant une largeur efficace de la semelle en béton conforme à 6.1.2. Pour les sections de Classe 4, il convient de déterminer la section efficace en acier conformément à l’EN 1993-1-5, 4.3,
- Dans le calcul de la résistance élastique à la flexion basé sur la section efficace, il convient d’adopter les limites de contraintes suivantes :
- fcd dans le béton comprimé ;
- fyd dans l’acier de construction tendu ou comprimé ;
- fsd dans l’armature tendue ou comprimée. En alternative, l’armature comprimée d’une dalle béton peut être négligée.
Calcul de l’axe neutre élastique
Dans le cas d’une section soumise à un moment de flexion négative, la contribution de la dalle en traction est négligée. On ne considère alors qu’un seul cas de la position de l’axe neutre élastique dans la section.
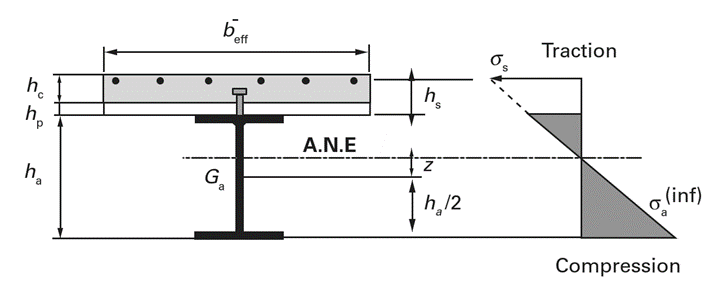
Une section mixte sous moment de flexion négatif résiste au niveau du profilé en acier et des barres d’armature comprises à l’intérieur de la largeur participante 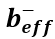 de la dalle.
de la dalle.
On désigne par AS l’aire totale des armatures participantes et par hS la cote de la nappe d’armatures par rapport à la face supérieure de la semelle du profilé (dans le cas d’une double nappe d’armatures, on peut adopter pour hS la cote du centre de gravité des nappes).
L’aire de la section mixte homogénéisée est :
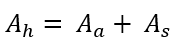
La distance Z de l’axe neutre élastique (ANE) au centre de gravité Ga de la section du profilé en acier est donnée par la formule suivante :
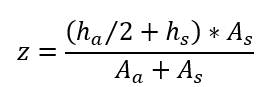
Le moment d’inertie géométrique de la section mixte homogénéisée par rapport à l’axe neutre est donné par l’expression suivante :
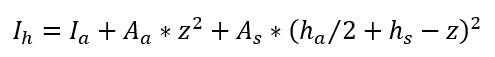
Calcul des contraintes de flexion
Les contraintes normales de flexion dues au moment sollicitant de calcul négative MEd s’obtiennent de la façon suivante :
- La contrainte de traction dans l’armature :
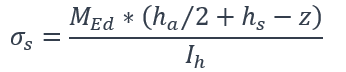
- La contrainte de traction dans la semelle supérieure de la poutre en acier :
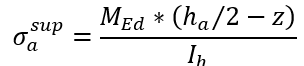
- La contrainte de compression dans la semelle inferieure du profile´ :
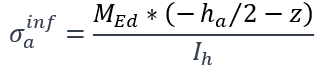
Les contraintes dépendent du cas de charge, du phasage et de l’état de résistance de la section.
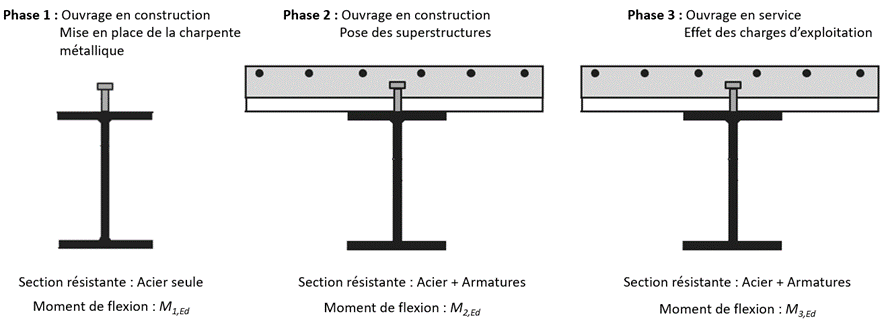
La contrainte totale s’écrit comme la somme de plusieurs états de contraintes.
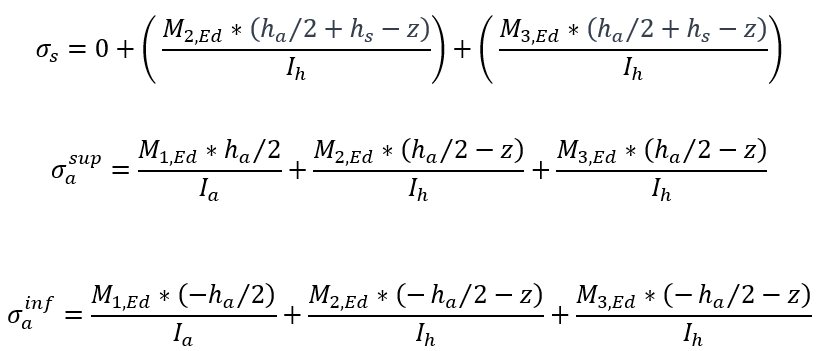
Avec :
M1,Ed Moment de flexion sous les charges de la phase 1.
M2,Ed Moment de flexion sous les charges de la phase 2.
M3,Ed Moment de flexion sous les charges de la phase 3.
Références bibliographiques
[1] NF EN 1994-1-1 : Eurocode 4 – Calcul des structures mixtes acier-béton – Partie 1 : Règles générales et règles pour les bâtiments. AFNOR. Juin 2005.
[2] NF EN 1992-1-1 : Eurocode 2 – Calcul des structures en béton – Partie 1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[3] Jean-Marie ARIBERT : Construction mixte acier-béton – Calcul des poutres mixtes de bâtiments – Partie 1 : poutres en T à âme pleine. Techniques de l’ingénieur. Août 2016
Noureddine Bouzidi, chef de projets – CTICM