Application du théorème de Barré aux poutres de roulement
Le théorème de Barré est un résultat bien connu en résistance des matériaux, qui permet de déterminer la position optimale d’un système de charges ponctuelles pour induire le moment de flexion le plus défavorable sur une poutre isostatique. Ce théorème est particulièrement utile dans le domaine des ouvrages d’art et des chemins de roulement, où les poutres sont soumises à des trains de charges ponctuelles.
Énoncé général
Soit une poutre posée sur deux appuis simples. Cette poutre est soumise à un chargement constitué de n charges ponctuelles verticales d’intensité quelconque, notées P0, P1, …, Pi, …, Pn. Soit R la résultante de ces charges. Soit Pk une charge quelconque choisie parmi ce système, le moment fléchissant dans la poutre est maximal au niveau de cette charge Pk lorsque la distance qui la sépare du milieu de la poutre est strictement égale à la moitié de celle qui la sépare de la résultante R, voir Figure 1.
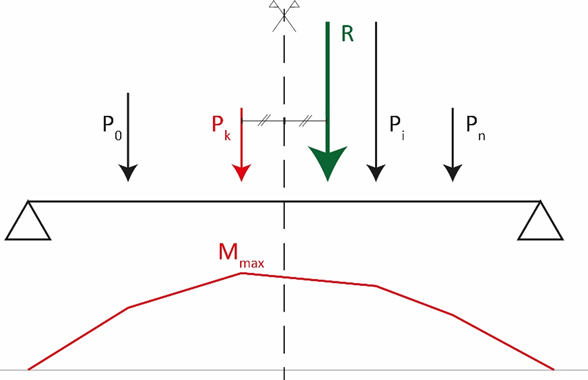
En supposant un système de charges mobiles, il est alors nécessaire de chercher le moment maximal au droit de chacune des charges du système afin de déterminer l’enveloppe de moment.
Cas d’un pont roulant à 4 galets
Appliquons maintenant le théorème au cas spécifique d’une poutre de roulement soumise aux actions verticales induites par un pont roulant à 4 galets, c’est-à-dire que deux charges verticales, espacées d’une distance a, se déplacent sur la poutre.
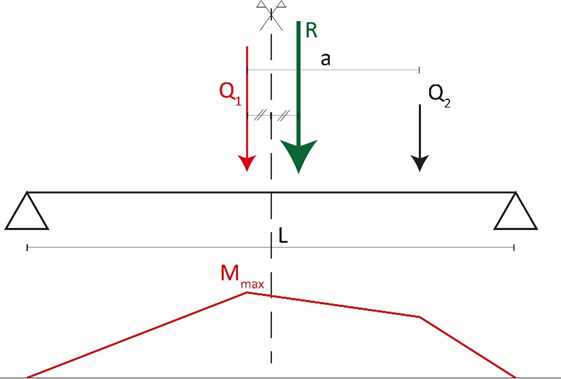
En supposant que les charges n’ont pas la même intensité, le moment fléchissant maximal qui peut se développer dans la poutre est obtenu en positionnant la charge la plus forte à la place décrite par le théorème. Elle doit donc être placée de telle manière que le milieu de la poutre soit à équidistance de la charge du galet et de la résultante verticale totale, voir Figure 2.
Lorsqu’il est possible de supposer que les charges des galets sont égales, le problème se simplifie. Le moment maximal est alors obtenu en plaçant l’un des galets à une distance exactement égale au quart de l’écartement entre galets a par rapport milieu de la poutre, voir Figure 3.
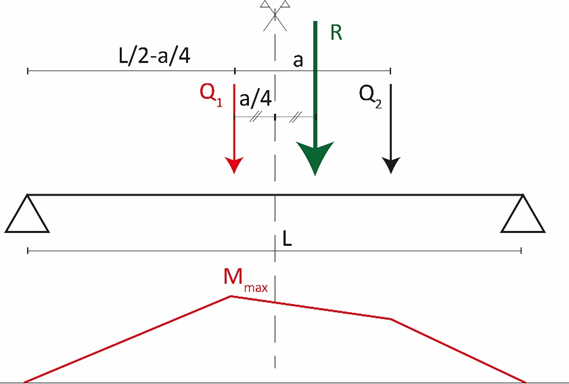
Mesurée depuis l’appui gauche de la poutre, la distance d à laquelle il convient de positionner le galet gauche (en rouge sur la figure) est donnée par la formule suivante :
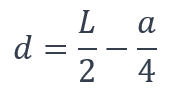
où
L : Longueur totale de la poutre,
a : Écartement des galets.
Et le moment maximal est obtenu par la formule suivante :
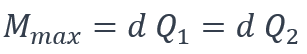
Romain Palacios – chef de projet recherche – CTICM