Module de résistance élastique au bimoment des profilés en U

Cet article a pour objectif de donner les formules de calcul du module de résistance élastique au bimoment des profilés en U à ailes parallèles (type UPE). Les valeurs numériques de ce paramètre calculées pour des profilés UPE courants sont également données.

Introduction

Les profilés en U qui sont soumis à la flexion par rapport à l’axe forte inertie, sont souvent sollicités en torsion. Si le calcul des contraintes normales dues à la flexion est bien connu, celui des contraintes normales dues à la torsion l’est moins. Ces contraintes peuvent être calculées par la formule suivante :

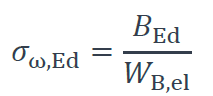
Où : B_Ed est la valeur de calcul du bimoment ;

W_B,el est le module de résistance élastique au bimoment, défini par :

I_w est l’inertie de gauchissement (ou inertie sectorielle) ;

ω_max est l’aire sectorielle maximale. Pour les profilés à section en U, l’aire sectorielle est maximale au bord libre des semelles (notée ω₀ ).

Les formules analytiques de I_w et de ω que l’on trouve dans la littérature (voir [1]) ont été établies avec l’hypothèse de contrainte normale constante suivant l’épaisseur des parois. Cette hypothèse est valable pour les profilés de section à parois minces dont le rapport largeur-épaisseur de la paroi est supérieur à 10. En revanche, pour les profilés laminés UPE courants dont le rapport largeur-épaisseur est inférieur à 10, la contrainte normale calculée avec ces formules de I_w et de ω peut ne pas être du côté de la sécurité. Cet article propose donc des formules de l’inertie de gauchissement et de l’aire sectorielle d’un profilé à section en U en supposant que la contrainte normale est linéaire suivant l’épaisseur des parois. Les congés de raccordement sont négligés dans les formules.

Inertie de gauchissement

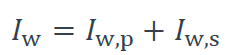
Où : I_w,p est l’inertie de gauchissement principale, établie avec l’hypothèse de contraintes normales constantes suivant l’épaisseur des parois (voir [1]) :

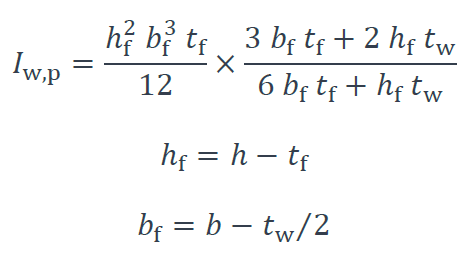
I_w,s est l’inertie de gauchissement secondaire, établie avec l’hypothèse de variation linéaire de contraintes normales suivant l’épaisseur des parois :

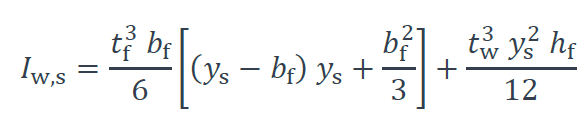
Aire sectorielle

Où : ω_0,p est l’aire sectorielle au bord libre de la semelle, établie avec l’hypothèse de contraintes normales constantes suivant l’épaisseur des parois (voir [1] ) :

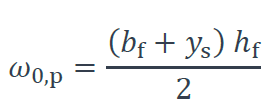
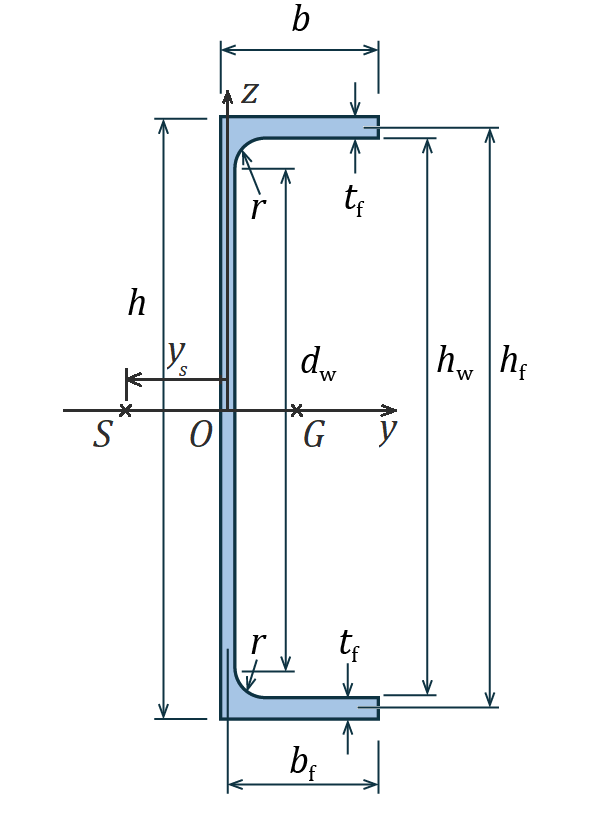
est la position du centre de cisaillement S dans le repère Oyz (voir Figure 1 ) :

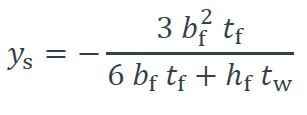
ω_0,s est l’aire sectorielle à la fibre intérieure du bord libre de la semelle, établie avec l’hypothèse de variation linéaire de contraintes normales suivant l’épaisseur des parois :

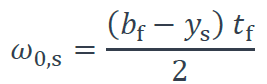
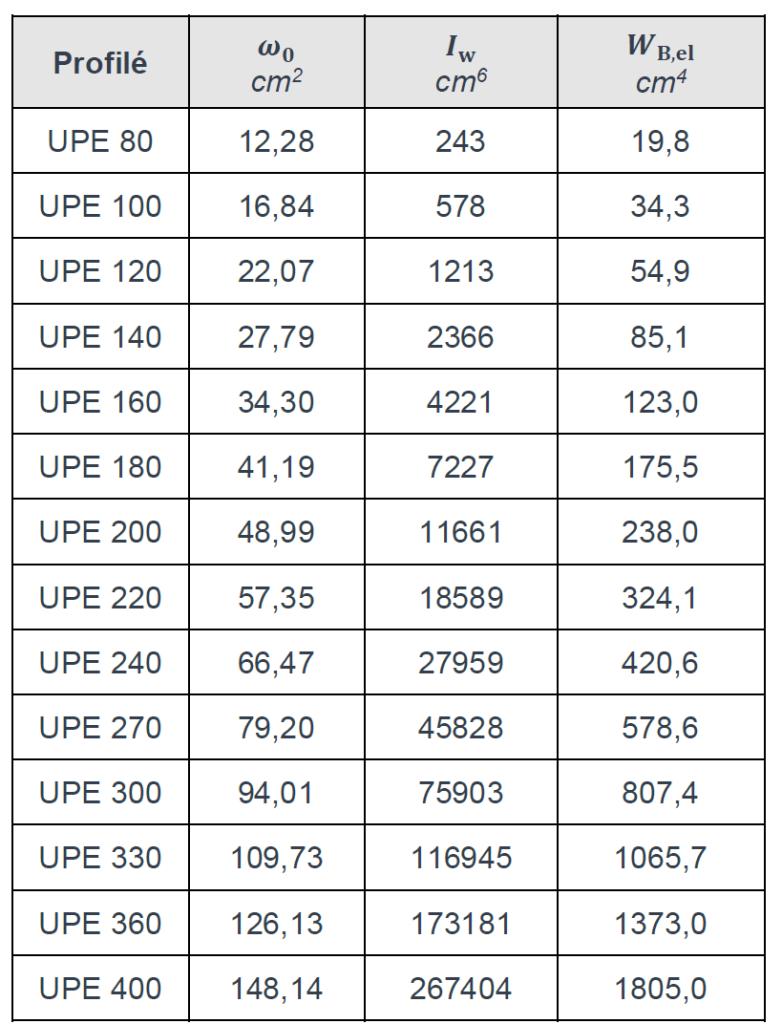
Aires sectorielles, inerties de gauchissement et modules de résistance élastique au bimoment des profilés UPE

Références

[1] J.T. Oden, E.A. Ripperger, « Mechanics of elastic structures », 2^nd edition, Hemisphere Publishing Corporation

Télécharger le document

Tien Minh Nguyen, chef de projet recherche– CTICM