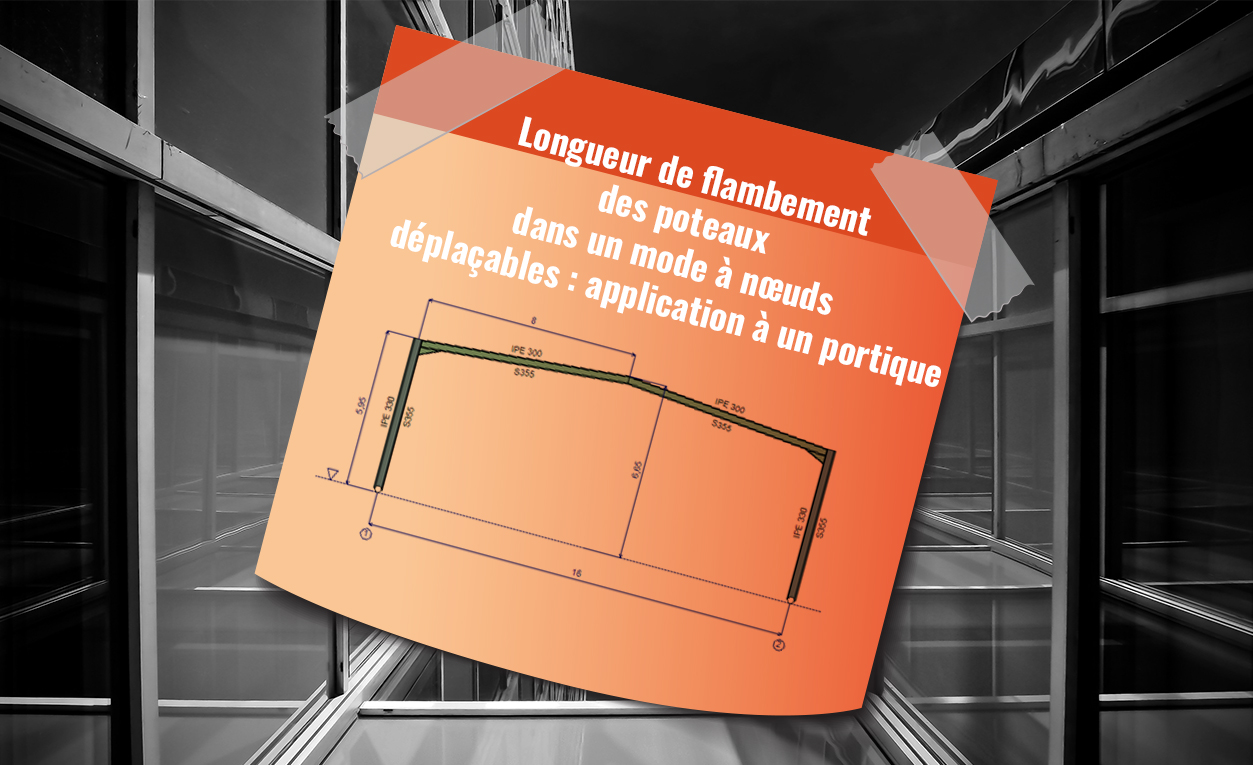
Longueur de flambement des poteaux dans un mode à nœuds fixes
La vérification d’une barre uniformément comprimée selon l’EN 1993-1-1 [1] requiert la détermination de son élancement réduit, qui dépend de sa longueur de flambement. Le présent article donne une méthode directe permettant d’évaluer la longueur de flambement dans le cas de portiques contreventés (mode d’instabilité à nœuds fixes).
NOTE La méthode présentée dans cet article, extraite de la référence [2], correspond à celle donnée dans la version expérimentale de l’Eurocode 3 [3], encore couramment employée en pratique, complétée de termes additionnels.
Domaine d’application
La méthode présentée ci-après est applicable dans le cadre des hypothèse suivantes :
- Barre à section constante et uniformément comprimée ;
- Structure poteaux – poutres à cadres réguliers avec assemblages rigides ;
- Mode d’instabilité globale de la structure à nœuds fixes.
La longueur de flambement d’une barre vérifiant ces hypothèses peut s’exprimer comme suit :
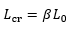
où β est le coefficient de longueur de flambement et L0 est la longueur d’épure de la barre.
NOTE Pour les barres ne vérifiant pas ces hypothèses, il convient de déterminer l’effort normal critique à partir d’une analyse par éléments finis de type bifurcation d’équilibre
Coefficient de longueur de flambement
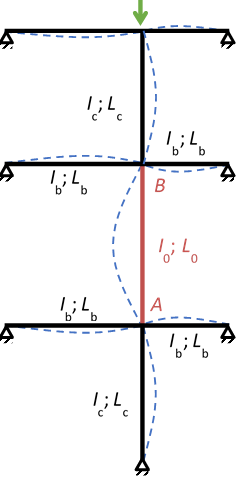
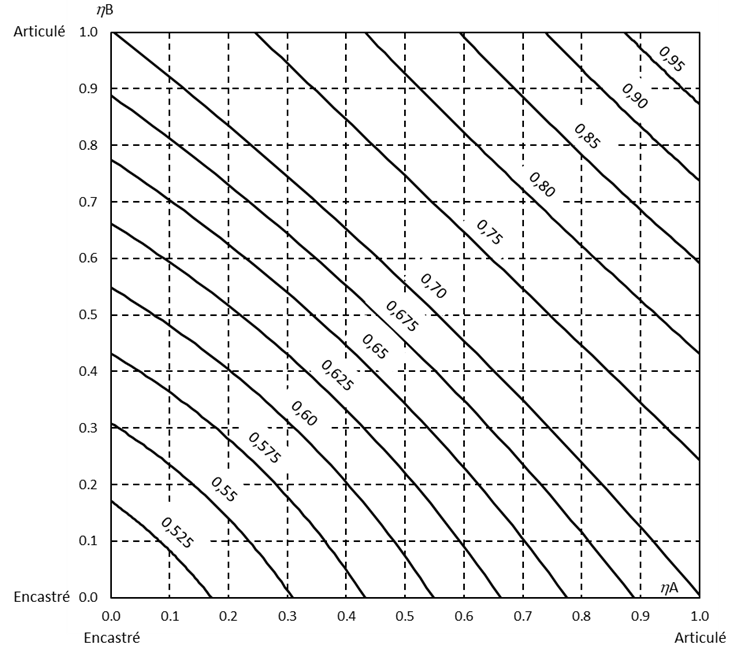
Le coefficient de longueur de flambement β du poteau AB (voir Figure 1) peut être déterminé à partir de l’abaque tracé à la Figure 2. Pour un calcul direct, l’expression suivante peut également être utilisée :
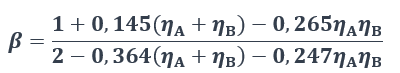
La valeur de β dépend des facteurs de distribution de rigidité ηA et ηB déterminés aux extrémités A et B de la barre respectivement.
NOTE Les expressions analytiques produisent des valeurs approchées des résultats obtenus à partir de l’abaque.
Facteurs de distribution de rigidité
Les facteurs de distribution de rigidité ηA et ηB, associés aux extrémités (ou nœuds) A et B du poteau, sont déterminés à partir de la même expression qui dépend des propriétés des barres aboutissant au nœud. Pour le nœud A, ce facteur est déterminé comme suit :
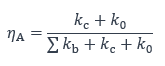
avec :
Indice « 0 » Poteau AB étudié (voir Figure 1) ;
Indice « c » Poteau aboutissant au nœud A et adjacent au poteau AB étudié ;
Indice « b » Poutres aboutissant au nœud A.
ki Raideur de la barre i du modèle déterminée comme suit :
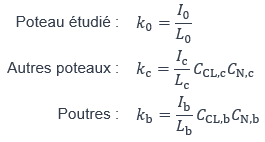
où :
I, L Inertie de flexion et longueur d’épure du poteau ou de la poutre aboutissant au nœud A ;
CCL Coefficient tenant compte des conditions de liaison à l’extrémité opposée du poteau ou de la poutre aboutissant au nœud A (voir Tableau 1);
CN Coefficient tenant compte de la présence d’effort normal de compression dans le poteau ou la poutre aboutissant au nœud A (voir Tableau 1).
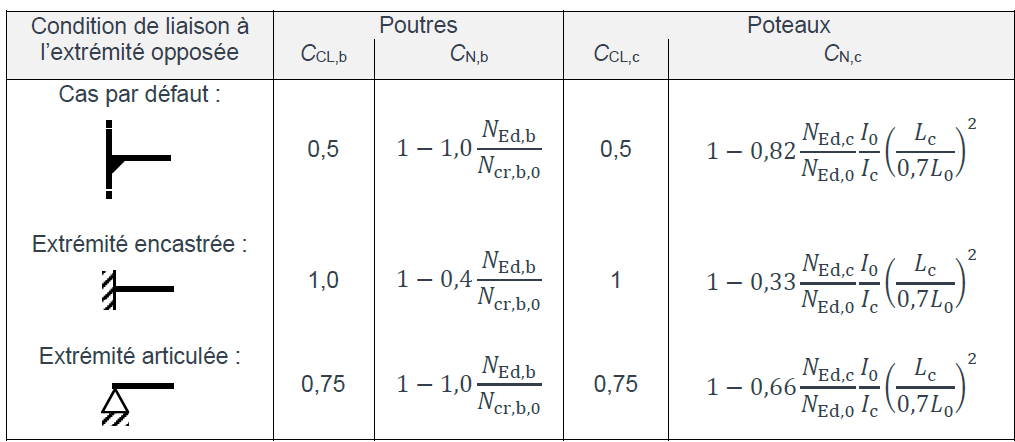
avec :
NEd Valeur de calcul de l’effort normal de compression agissant dans la poutre ou dans le poteau. La possible présence d’un effort normal de traction est négligée.
Ncr,b,0 Valeur de l’effort normal critique de la poutre, supposée bi-articulée, pour le flambement par flexion dans le plan du portique.
Utilisation pour l’analyse globale
Dans le cadre de l’analyse globale selon l’Eurocode 3 Partie 1-1 [1], il est possible de vérifier la résistance au flambement des poteaux en utilisant une longueur de flambement à nœuds déplaçables. Cette méthode permet de se limiter à une analyse globale au 1er ordre sans prise en compte des imperfections. Les conditions d’application de cette méthode d’analyse globale sont décrites dans l’article [4] (Méthode EM).
Références
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[2] Lebastard, M. (2024) Longueur de flambement des poteaux dans le plan d’un portique. Revue construction métallique 3-2024.
[3] CEN. (1992) ENV 1993-1-1 : Eurocode 3 « Calcul des structures en acier » et document d’application nationale – Partie 1-1 : Règles générales et règles pour les bâtiments.
Maxime Lebastard, ingénieur de recherche – CTICM