Dans un profil ouvert, la torsion engendre des contraintes normales et des contraintes de cisaillement. Cet article présente une méthode simplifiée pour évaluer de façon sécuritaire ces contraintes dans une section en I ou H doublement symétrique.
Rappel sur la torsion
De manière générale, un moment de torsion appliqué à une barre droite génère un effort interne de torsion T qui est la somme de deux composantes :
Tt moment de torsion uniforme (théorie de Saint Venant) ;
Tw moment de torsion non uniforme (théorie de Vlassov) ;
À l’abscisse x, l’effort interne de torsion est : T(x)=Tt (x)+Tw (x) Dans une section en I ou H, le moment de torsion uniforme engendre des contraintes de cisaillement dans toute la section alors que le moment de torsion non uniforme engendre dans les semelles, des contraintes de cisaillement et, par l’intermédiaire du bimoment (flexion dans le plan des semelles), des contraintes normales. Dans la norme NF EN 1993-1-1 [1], il est précisé en 6.2.7(7) que la part de torsion uniforme peut être négligée dans les calculs pour un profil ouvert. Cette hypothèse simplificatrice revient donc à considérer :
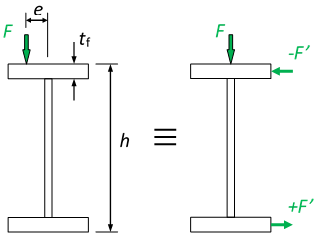
T(x)=Tw (x) Prenons le cas d’une charge F appliquée à une abscisse xF d’une poutre à section en I, avec un excentrement e. La torsion provoquée par cet excentrement peut être représentée par un couple C de forces appliquées dans le plan des semelles comme représenté à la Figure 1. Ce qui conduit à :
C=F e=F’ (h-tf)
Où :
h est la hauteur totale de la section ;
tf est l’épaisseur des semelles.
Figure 1 – Couple de forces équivalent à la torsion provoquée par une charge excentrée
En isolant une des semelles, la force F’ engendre de la flexion dans le plan de cette semelle. Il est alors aisé de calculer le moment de flexion Mfz(x), l’effort tranchant Vf(x) et les contraintes qui en résultent, dans toute section d’abscisse x sur la longueur de cette semelle, en tenant compte des conditions d’appui dans le plan horizontal.
Note : la référence [2] décrit la méthode pour un calcul détaillé d’une poutre sollicitée en torsion.
Exemple d’application
Considérons une poutre PRS telle que décrite à la Figure 2. Cette poutre sur appuis simples a une portée L = 5 m. Au droit de ses deux appuis, la poutre est maintenue latéralement et le gauchissement est libre. Elle supporte une charge concentrée verticale, F = 20 kN, à mi-portée. Cette charge est excentrée de e=12mm par rapport au plan moyen de l’âme.
Figure 2 – Poutre soumise à une charge concentrée, excentrée par rapport à l’âme
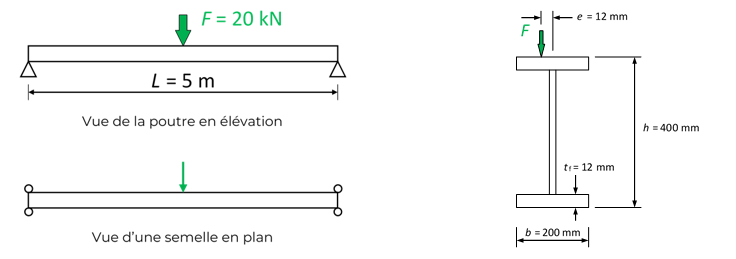
Le moment de torsion appliqué à la poutre est donc :
F e=20×0,012=0,24 kN.m
Ce moment de torsion peut être représenté par deux forces opposées, F’ et –F’, agissant chacune dans le plan moyen d’une semelle :
F‘=(F e)/(h-tf )=0,24/(0,400-0,012)=0,6185 kN
Le moment fléchissant maximal dans le plan d’une semelle est obtenu par :
Mfz=F’L/4=(0,6185×5)/4=0,7731 kN.m
Bien qu’il ne soit pas exclu de se référer à la résistance plastique pour une poutre sollicitée en torsion, il est conseillé de se limiter à sa résistance élastique. Il est ensuite aisé de calculer les contraintes équivalentes de von Mises en différents points d’une section, pour tenir compte des différentes contraintes qui résultent des autres sollicitations (effort axial, moment de flexion, effort tranchant). Il s’agira ensuite de vérifier que la valeur maximale de la contrainte équivalente de von Mises ne dépasse pas la limite d’élasticité de calcul. Le module de résistance élastique de la semelle pour la flexion dans son plan est :
Wfz=(tf b2)/6=(12×2002)/6×10-3=80 cm3
La contrainte normale maximale dans la semelle due au moment de torsion est obtenue à mi-portée :
σmax=Mfz/Wfz =(0,7731×106)/80000=9,7 MPa
L’effort tranchant dans le plan de la semelle est :
Vf=F’/2=0,6185/2=0,309 kN
La contrainte de cisaillement maximale dans la semelle due au moment de torsion est :
Les diagrammes des contraintes normales et des contraintes de cisaillement dans les semelles sont représentés à la Figure 3.
Figure 3 – Diagrammes des contraintes dans les semelles
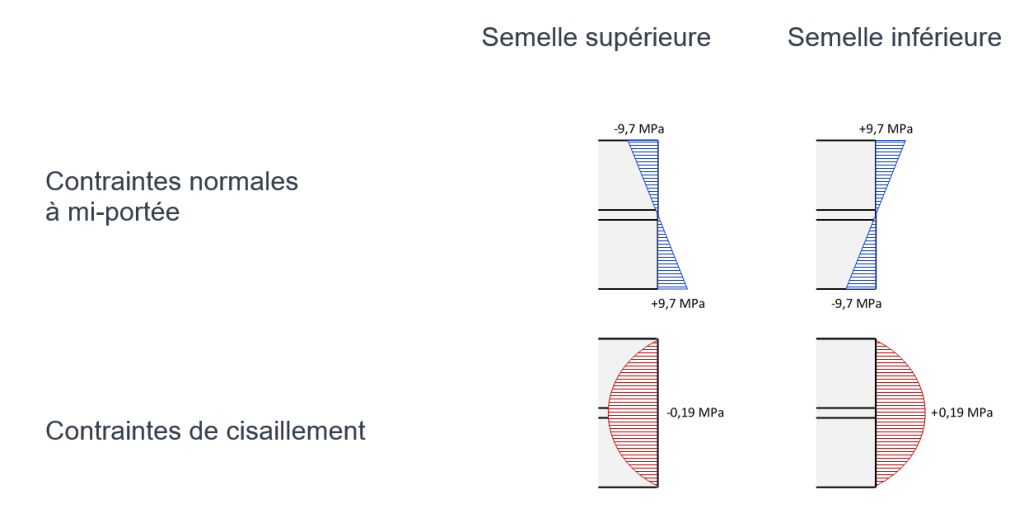
Le tableau suivant présente une comparaison entre les valeurs des contraintes obtenues précédemment et celles obtenues par un calcul plus précis tenant compte de la torsion uniforme. Ces dernières ont été calculées avec le programme TORSION [4] dont la formulation est donnée dans la référence [3].
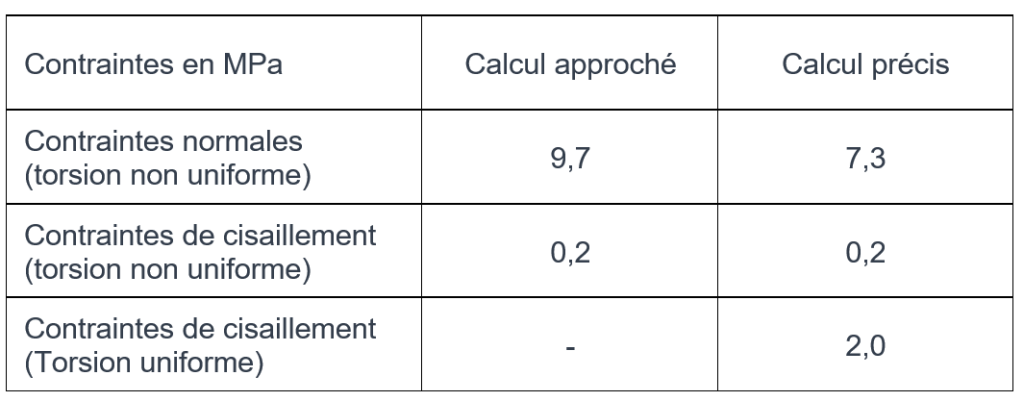
Il convient de noter les tendances suivantes pour les profils ouverts :
les contraintes normales dues à la torsion sont généralement significatives;
les contraintes de cisaillement dues à la torsion sont souvent assez faibles ;
la méthode simplifiée tend à surestimer les contraintes normales, surtout pour les sections massives (parois peu élancées).
Note : une poutre sollicitée en flexion et en torsion doit être vérifiée vis-à-vis du déversement. La présente note ne couvre pas cette vérification qui pourra faire l’objet d’une future note.
Références
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[2] BARAKA S., BUREAU A., Calcul des contraintes dues à la torsion. Revue Construction Métallique 1-2000, p. 85-100. CTICM.
[3] NGUYEN T. M., Formulaire des contraintes dues à la torsion dans une poutre à section ouverte. Revue Construction Métallique 4-2013, p. 45-75. CTICM.
[4] Logiciel TORSION. Disponible en téléchargement libre sur le site cticm.com: ici
