Résistance au déversement des poutres à section en U

Cet article propose une méthode pratique issue de travaux de recherche [1] permettant de déterminer le moment résistant au déversement des profilés laminés à section en U.

Généralités

Le calcul de la résistance au déversement des poutres laminées à section en U selon l’EN 1993-1-1 [2] requiert l’utilisation de la courbe de flambement d. Cette méthode peut également être utilisée mais peut s’avérer insécuritaire pour les faibles élancements et particulièrement sécuritaire pour les élancements intermédiaires et élevés, plus courants en pratique.

La méthode décrite dans le présent article a été intégrée dans le projet de révision de l’Annexe nationale à l’Eurocode 3 Partie 1-1 [3].

Cette méthode n’est pas applicable aux profils formés à froid. Pour ces éléments, le lecteur se reportera à l’Eurocode 3 Partie 1-3 [4].

Méthode de calcul

La stabilité des poutres constituées par un profilé laminé à chaud à section en U constante (gammes UPE et UPN de la norme NF EN 10365 [5]) vis-à-vis du déversement est satisfaite lorsque la condition suivante est vérifiée :

où :

avec :

• M_y,Ed    Valeur de calcul du moment fléchissant autour de l’axe de forte inertie ;
• Wy       Module de résistance de la section transversale pour la flexion autour de l’axe de forte inertie, donné par [2] :
  • Sections de Classe 1 ou 2 : W_y = W_pl,y (module plastique) ;
  • Sections de Classe 3 : W_y = W_el,y (module élastique) ;
  • Sections de Classe 4 : W_y = W_eff,y (module efficace) ;
• f_y         Limite d’élasticité de l’acier ;
• γ_M1       Coefficient partiel pour la résistance des barres aux instabilités (g_M1 = 1,0 pour les structures de bâtiments) ;
• M_cr       Moment critique de déversement élastique de la poutre, qui peut être déterminé à partir de la méthode de l’Annexe M de l’Annexe nationale à l’EN 1993-1-1 [6].

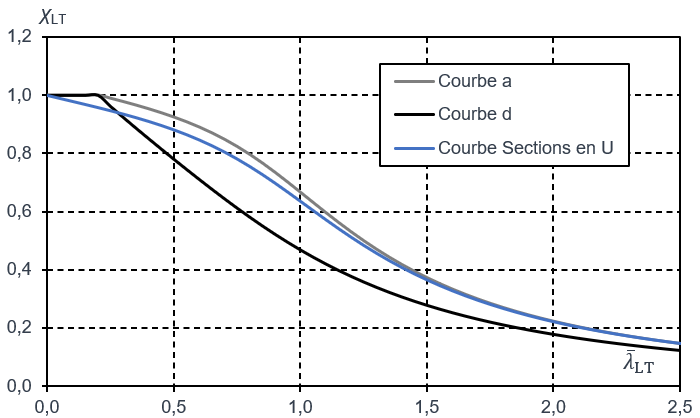
La courbe de déversement associée à la méthode présentée dans cet article est comparée aux courbes a et d de l’EN 1993-1-1 [2] à la Figure 1 ci-dessous.

La condition de stabilité donnée ne tient compte que du moment de flexion autour de l’axe de forte inertie. En pratique, les poutres à section en U sont souvent soumises à un chargement transversal appliqué hors du centre de cisaillement de la section. L’excentrement du chargement par rapport au centre de cisaillement de la section transversale produit alors un moment de torsion.

Dans ce cas, il convient de vérifier également la stabilité de la poutre sous l’effet de l’interaction entre le moment de flexion et le moment de torsion. Cette vérification fera l’objet d’un prochain article.

Références

[1] BEYER A., KHELIL A., BOISSONNADE N., BUREAU A. Résistance des profilés U laminés soumis à la flexion et la torsion – Partie II : Etude paramétrique et modèle de calcul. Revue construction métallique 3-2021, p. 95-133.

[2] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.

[3] prNF EN 1993-1-1/NA : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe nationale à la NF EN 1993-1-1. 2024. En cours de rédaction.

[4] NF EN 1993-1-3 : Eurocode 3- Calcul des structures en acier – Partie 1-3 : règles générales – Règles supplémentaires pour les profilés et plaques formés à froid. AFNOR. Mars 2007.

[5] NF EN 10365 : Profilés en U en aciers laminés à chaud, poutrelles I et H – Dimensions et masses. AFNOR Mars 2017.

[6] NF EN 1993-1-1/NA : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe nationale à la NF EN 1993-1-1. AFNOR. Août 2013.

Télécharger le document

Maxime Lebastard, ingénieur de recherche – CTICM