Calcul sismique simple par comparaison des descentes de charges vent et séisme #2

Pour certaines structures légères situées en zone sismique, comme les bâtiments industriels, le dimensionnement de l’ossature peut être gouverné par le vent plus que par le séisme. La clause 4.4.1 (2) de la norme NF EN 1998-1 permet dans ce cas de justifier le calcul sismique par une simple comparaison des descentes de charge dues au vent et au séisme.

Cet article comprend les trois parties suivantes :

• Partie I :       Principes de la méthode et données de l’exemple traité
• Partie II :      Calcul de l’action sismique
• Partie III :     Calcul de l’action du vent et synthèse

Les références sont données dans la partie III.

Hypothèses de calcul

La méthode doit être appliquée en considérant le bâtiment comme étant de classe de ductilité DCL avec un coefficient de comportement q = 1,5. On notera en outre que la prise en compte d’une torsion accidentelle ne modifie pas la descente de charge globale.

Pour le calcul au vent, on néglige la possibilité offerte par la NF EN 1991-1-4 de réduire la charge globale du vent pour défaut de corrélation des faces au vent et sous le vent (clause 5.3 (4) de la norme).

Le coefficient de défaut de corrélation pour le calcul de la charge globale du vent sur un bâtiment permet de réduire la descente de charge. Il n’est pas obligatoire de le prendre en compte. Pour l’application de la méthode simplifiée présentée dans cette fiche, ce coefficient peut être pris en compte ou non, au choix de l’ingénieur de calcul. Dans une stratégie visant à justifier autant que possible la résistance d’un bâtiment à partir du seul calcul au vent, il peut être opportun d’omettre cette réduction.

Descente de charges sous l’action du séisme – direction transversale

Le bâtiment est ici étudié pour le séisme agissant dans la direction transversale (direction y sur la Figure 2 en Partie I), pour laquelle la stabilité de l’ossature est assurée par les huit portiques.

Il convient tout d’abord de calculer la période propre du mode fondamental du bâtiment. Compte tenu de la présence des poutres au vent longitudinales, tous les portiques contribuent de manière identique à la reprise des charges transversales, donc des charges sismiques. De ce fait, on peut calculer la période propre du bâtiment en se ramenant à l’étude d’un portique simple, avec une masse en tête égale à 1/8 de la masse totale en tête du bâtiment (m_sup).

La période propre d’un portique simple avec pieds de poteaux articulés peut être calculée par la formule suivante (cf. formulaire [5]) :

où :      m est la masse en tête du portique ;

h est la hauteur des poteaux ;

E est le module d’Young de l’acier ;

I_c est le moment d’inertie des poteaux ;

ρ_k est un coefficient de raideur, déterminé de la manière suivante :

k est le coefficient de raideur relative des poteaux et de la traverse, défini par :

I_b est le moment d’inertie de la traverse ;

L est la portée de la traverse.

En prenant bien soin d’effectuer les calculs avec des unités homogènes (le mètre pour la longueur, le newton pour la force et le kilogramme pour la masse afin d’obtenir la période en secondes), les valeurs obtenues sont les suivantes :

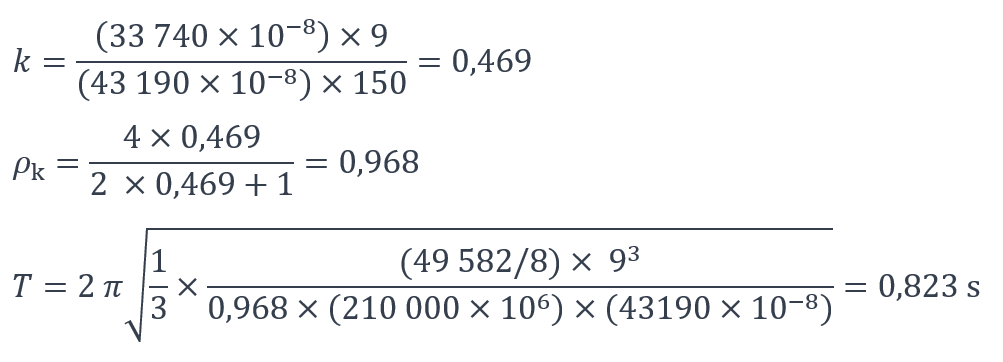
L’accélération sismique associée à cette période propre peut être calculée à partir des formules du spectre de calcul du paragraphe 3.2.2.5 de la NF EN 1998-1 [1]. Puisque T est compris entre T_C = 0,4 s et T_D = 2 s, c’est la formule (3.15) de la norme qui s’applique :

où :      a_g est l’accélération de calcul pour un sol de classe A, définie par :

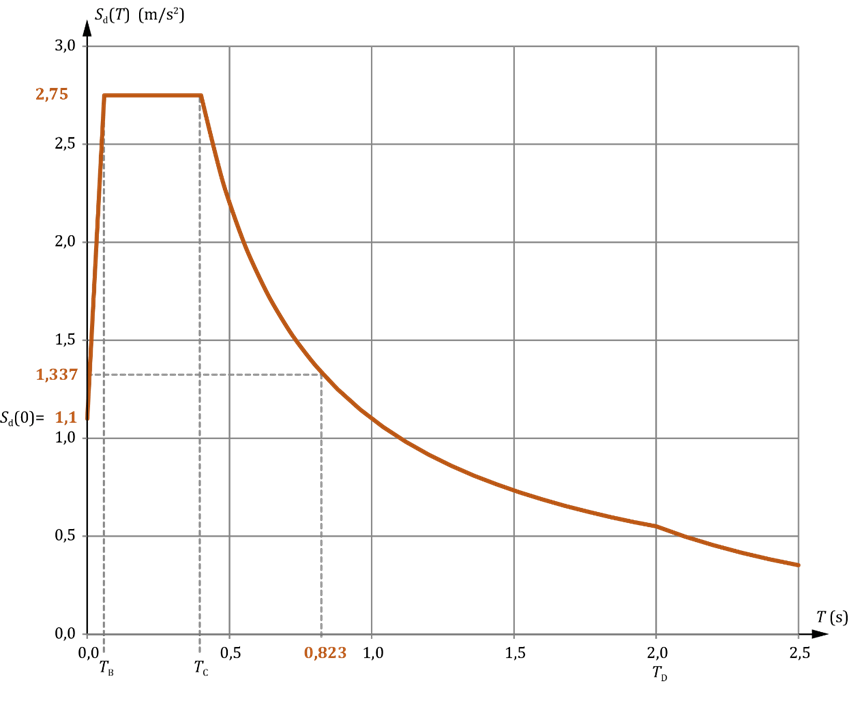
Pour le bâtiment étudié, les calculs conduisent aux résultats suivants (Figure 4) :

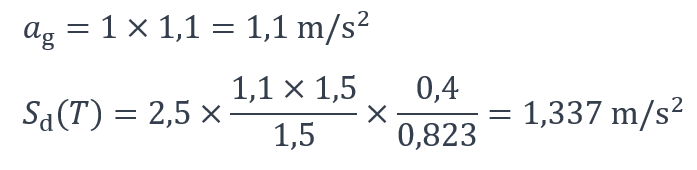
Le bâtiment ne comporte qu’un seul niveau et il ne présente pas d’irrégularité au sens de la NF EN 1998-1, ni en plan ni en élévation. La descente de charges sismiques globale pour le bâtiment peut alors se déterminer de la manière suivante :

• la masse rattachée à la toiture, m_sup, subit une accélération sismique égale à S_d(T), ce qui correspond à un effort tranchant à la base égal à m_sup S_d(T) ;
• la masse rattachée aux fondations, m_inf, subit une accélération sismique égale à celle du sol (c’est-à-dire S_d(0), l’accélération spectrale pour une période nulle), ce qui correspond à un effort tranchant égal à m_inf S_d(0).

Finalement, l’effort tranchant total à la base du bâtiment sous l’effet du séisme est calculé à l’aide de la formule suivante :

L’accélération spectrale pour une période nulle est calculée à l’aide de la formule (3.13) de la NF EN 1998-1, en considérant T = 0 :

Pour le bâtiment étudié, l’application de ces formules conduit aux résultats suivants :

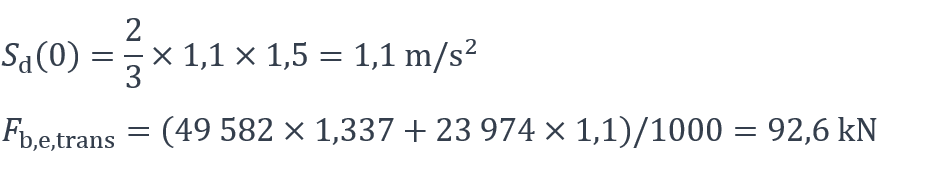
Descente de charges sous l’action du séisme – direction longitudinale

Pour le séisme agissant dans la direction longitudinale (direction x sur la Figure 2 en Partie I), la stabilité du bâtiment est assurée par la palée de contreventement transversale située dans la travée centrale. Ce type de contreventement est généralement raide, de telle sorte qu’il est raisonnable de supposer que la période propre pour cette direction soit proche du plateau du spectre de calcul (Figure 4), c’est-à-dire proche de T_C. De manière qui place du côté de la sécurité, l’accélération sismique correspondante au plateau du spectre est donc adoptée (formule (3.14) de la NF EN 1998-1) :

Ce qui donne la valeur suivante :

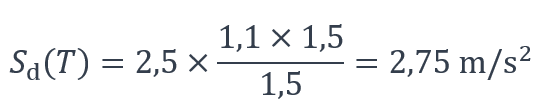
L’effort tranchant longitudinal à la base du bâtiment est calculé à l’aide de la formule (8), ce qui donne le résultat suivant :

À suivre : Partie III :       Calcul de l’action du vent et synthèse

Télécharger le document

Pierre-Olivier Martin, directeur de projet recherche, CTICM