Tout savoir sur
la construction métallique
La connaissance du comportement moment-rotation des assemblages est nécessaire pour l’analyse des ossatures métalliques. Cette fiche présente quelques aspects généraux sur ce point et sera suivi par une autre fiche détaillant la « méthode des composants » utilisée dans l’Eurocode 3 partie 1-8 pour déterminer la rigidité des assemblages.
Un assemblage est une zone où deux barres ou plus sont connectées entre elles, de façon à assurer la transmission de sollicitations bien identifiées d’un élément à l’autre. En deux dimensions, les deux modèles idéalisés d’assemblages les plus utilisées sont :
Le comportement d’un assemblage réel sollicité en flexion se situe toujours entre ces deux situations extrêmes théoriques. La connaissance de ce comportement est nécessaire afin de s’assurer de la bonne cohérence du modèle de calcul avec l’ouvrage à construire (ou construit dans le cas d’un existant).
La figure ci-dessous montre des exemples de courbes de comportement en flexion de quelques assemblages pouvant être rencontrés en pratique. Une telle courbe décrit l’évolution du moment fléchissant au sein de l’assemblage en fonction de la rotation de ce dernier. Cette courbe dite « de comportement » est une droite confondue avec l’axe des abscisses dans le cas de l’articulation parfaite ou avec l’axe des ordonnées dans le cas de la continuité parfaite.
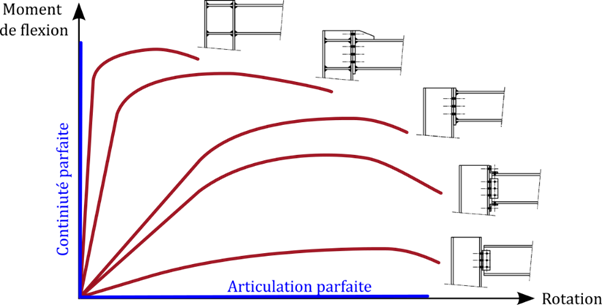
En construction métallique, la pratique courante consiste à modéliser l’assemblage lors de l’analyse globale comme une articulation ou comme un encastrement, en fonction de sa position au sein de la structure, puis de mettre en œuvre, lors de l’exécution, les dispositions constructives adéquates afin d’obtenir un comportement au plus proche de l’hypothèse prise au départ. Historiquement, ces « dispositions constructives adéquates » correspondaient à des règles de l’art plus ou moins formalisées.
Dans le cadre de l’Eurocode 3 partie 1-8, le comportement en rotation d’un assemblage est représenté par une courbe idéalisée représentée à la figure ci-dessous.
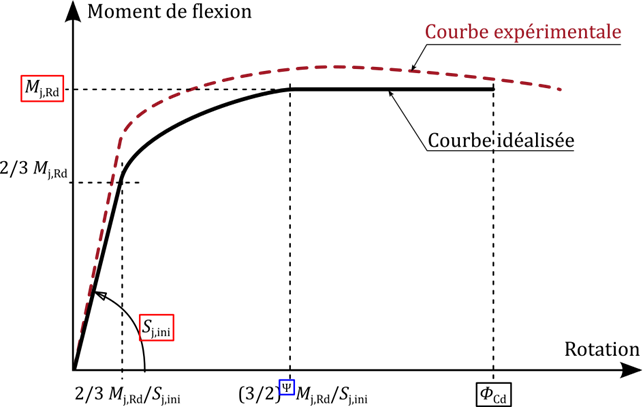
Cette courbe comprend trois paramètres essentiels :
Le paramètre Ψ est donné dans l’Eurocode en fonction du type d’assemblage (Ψ = 2,7 dans la plupart des cas). A noter que la prise en compte du comportement de l’assemblage dans une analyse peut se faire en utilisant des modèles simplifiés (ressort élastique en rotation), au lieu de la courbe idéalisée non linéaire montrée plus haut.
Il existe différentes méthodes permettant de connaitre le comportement moment–rotation d’un assemblage, la référence [2] en propose une revue qui est synthétisée ci-dessous, et complétée sur certains aspects.
Tout d’abord, il est évidemment possible de réaliser un essai sur l’assemblage dont on souhaite connaitre le comportement, voir la figure ci-dessous. Par principe, il s’agit d’une méthode permettant d’approcher au mieux la « réalité ». Cependant, cela se révèle couteux et difficilement généralisable. Il est en effet nécessaire de réaliser de nouveaux essais à chaque modification dans la conception.
Une campagne expérimentale incluant plusieurs d’assemblages différents, mais de conception similaire, peut permettre d’obtenir une réponse un peu plus générale sous forme de lois empiriques. De telles expressions permettent de prévoir le comportement d’un assemblage n’ayant pas été testé, tant qu’il présente une conception similaire et des paramètres (dimensions, épaisseurs, matériaux, etc.) inclus dans le domaine de validité de l’étude initiale.
Il est possible de substituer un essai par une analyse numérique par éléments finis (EF), voir la figure ci-dessous, moins chère et présentant un meilleur potentiel de généralisation grâce à des outils de modélisation paramétrique. Cette méthode était historiquement couteuse en temps machine, mais ce défaut n’est plus vraiment rédhibitoire aujourd’hui. Elle nécessite cependant des compétences pointues pour être mise en œuvre avec les codes EF généralistes.
Ces dernières années ont vu se développer de nouveaux outils dédiés à l’étude des assemblages en acier par éléments finis. Le plus répandu actuellement utilise une démarche mélangeant éléments finis et méthode des composants. Si de tels outils rendent la modélisation EF d’assemblages largement plus accessibles, des connaissances solides concernant à la fois le comportement des assemblages et les éléments finis restent indispensables à leur utilisation en sécurité.
Le principe général de la méthode de composants est simple : le comportement général d’un assemblage peut être déduit des propriétés mécaniques de ses différents composants [3].
Cette méthode permet au concepteur de déterminer analytiquement le comportement de n’importe quel assemblage en décomposant ce dernier en plusieurs sous éléments pertinents, appelés « composants ». Ensuite le comportement individuel de chaque composant est agrégé dans un modèle mécanique, voir la figure ci-dessus, qui permet d’en déduire le comportement de l’assemblage complet.
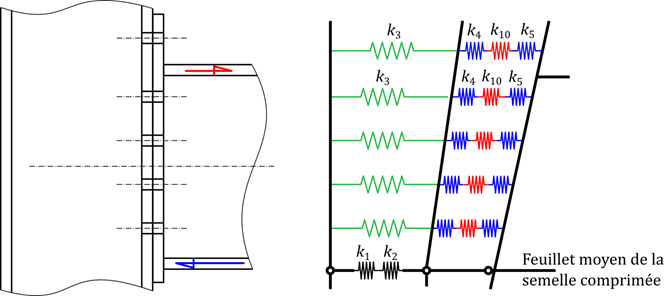
En pratique, il y a une limite évidente : le comportement de chaque composant pertinent doit être caractérisé pour pouvoir appliquer la méthode. Cette caractérisation peut être réalisée en analysant le comportement mécanique de chaque composant, par exemple dans le cadre de la théorie des poutres. Des essais ou des simulations numériques permettent ensuite de vérifier la bonne cohérence des résultats obtenus, voire de procéder à une calibration empirique si nécessaire.
Il s’agit de la méthode utilisée par l’Eurocode 3 partie 1-8 pour déterminer la rigidité initiale d’un assemblage. Une présentation détaillée de cette démarche est l’objet d’une fiche à venir [4].
Divers travaux de recherche étendent la méthode des composants pour la détermination d’autres paramètres de la courbe de comportement, comme la capacité de rotation.
La référence [2] cite également les modèles analytiques, c’est-à-dire des formules construites sur la base des concepts de base de l’analyse des structures. Cette méthode s’approche des modèles mécaniques mais dans une version moins systématique, dans le sens où seulement certains « composants » (les plus pertinents) sont pris en compte. Elle permet généralement d’obtenir certains paramètres de la courbe de comportement (la rigidité et/ou le moment résistant par exemple), mais pas forcément toute la courbe.
Enfin, la référence [2] envisage dès 2011 l’usage de l’intelligence artificielle, via l’emploi de réseaux de neurones. Si les progrès des réseaux de neurones ont été spectaculaires dans bien des domaines ces dernières décennies, leur usage pour le calcul d’ossatures reste encore limité en dehors de la R&D.
[1] NF EN 1993-1-8 (2005) : Eurocode 3 – Calcul des structures en acier. Partie 1-8 : Calcul des assemblages. AFNOR. Décembre 2005.
[2] DIAZ C, MARTI P, VICTORIA M, QUERIN O (2011). Review on the modelling of joint behaviour in steel frames. Journal of Constructional Steel Research. Vol. 67, pp 741-758.
[3] WEYNAND K, JASPART J.-P., STEENHUIS M. (1996). The stiffness model of revised Annex J of Eurocode 3. Connections in Steel Structures III, p. 441-452.
[4] A. RODIER. Rigidité d’un assemblage par la méthode des composants. Article Métalétech à paraître.
Anthony Rodier, chef du service formation, CTICM