Rigidité d’un assemblage par la méthode des composants

L’Eurocode 3 partie 1-8 [1] fournit une démarche permettant de déterminer la rigidité initiale en rotation d’assemblages courants en flexion. Le modèle de la norme utilise la « méthode des composants », un ensemble de concepts que la présente fiche propose d’expliquer.

Principe général de la méthode des composants

En théorie, la méthode des composants permet au concepteur de déterminer analytiquement le comportement de n’importe quel assemblage en décomposant ce dernier en plusieurs sous éléments pertinents, appelés « composants ». Ensuite le comportement individuel de chaque composant est agrégé dans un modèle mécanique qui permet d’en déduire le comportement de l’assemblage complet. En pratique, il y a une limite évidente : le comportement de chaque composant pertinent doit être caractérisé pour pouvoir appliquer la méthode.

Dans le cadre de l’Eurocode 3 partie 1-8 [1], le comportement élastique des composants d’assemblage les plus courants est directement décrit sous la forme de coefficients de rigidité k_i. Grâce à cette caractérisation, il est possible de déterminer analytiquement la rigidité initiale en rotation d’un assemblage classique. Dans l’Eurocode 3 partie 1-8, les coefficients de rigidité k_i sont définis par la relation ci-dessous :

Où Δ_i représente la déformation du composant i sous un effort F_i, et E le module d’Young de l’acier (210 000 MPa). Il ne s’agit donc pas de coefficients au sens strict, car ils sont homogènes à une longueur (usuellement exprimée en mm).

Ces coefficients de rigidité peuvent être déterminés analytiquement, expérimentalement ou empiriquement, selon le cas. Ils sont ensuite agrégés dans un modèle mécanique comportant des ressorts en série et parallèle tel que celui décrit au paragraphe suivant.

Composants d’assemblage courants

Afin de déterminer la rigidité initiale en rotation d’un assemblage, la démarche débute par l’identification des composants qui le constituent. Les différents composants traités dans l’Eurocode 3 partie 1-8 sont listés dans le tableau 6.1 de cette norme [1].

La force de la méthode des composants est de pouvoir s’adapter à tout type de conception tant que les composants sont bien caractérisés. L’Eurocode 3 liste une vingtaine de composants qui permettent de traiter les assemblages les plus courants. La démarche générale est applicable à d’autres cas, à condition de rechercher les coefficients de rigidité dans d’autres références. Il convient alors de porter une attention particulière sur la bonne compatibilité de telles expressions avec l’Eurocode et son niveau de sécurité attendu.

La figure ci-dessous montre comment un assemblage poutre-poteau par platine d’about boulonnée peut être représenté sous la forme d’un ensemble de composants.

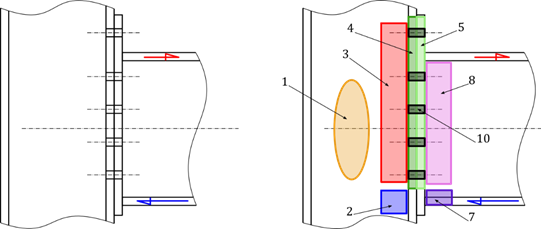
Pour un tel assemblage, les composants suivants peuvent être identifiés :

1- Panneau d’âme du poteau en cisaillement – k₁

2- Âme du poteau en compression transversale – k₂

3- Âme du poteau en traction transversale – k₃

4- Semelle du poteau en flexion – k₄

5 -Platine d’about en flexion – k₅

6- Semelle et âme de la poutre en compression – k₇

7- Âme de la poutre en traction – k₈

8- Boulons en traction – k₁₀

Les différents coefficients de rigidité sont actuellement identifiés par des numéros, mais il est prévu de modifier cela dans la révision de l’Eurocode 3 partie 1-8. Par exemple, le coefficient k₁ deviendrait k_wp (wp pour « web panel »).

Un certain nombre de composants sont définis avec un coefficient de rigidité égal à l’infini (voir les notes du tableau 6.11) [1]. C’est le cas de la semelle et de l’âme de la poutre en compression (k₇), de l’âme de la poutre en traction (k₈) ou encore des soudures (k₁₉ – non représenté sur la figure).

C’est également le cas de l’âme du poteau en compression transversale (k₂) si un raidisseur est mis en place en vis-à-vis de la semelle comprimée de la poutre. Ces composants ont une influence négligeable sur la déformation de l’assemblage.

Construction du modèle mécanique et détermination de la rigidité

Il est possible de construire un modèle mécanique comme montré sur la figure ci-dessous pour un assemblage poutre-poteau par platine d’about boulonnée.

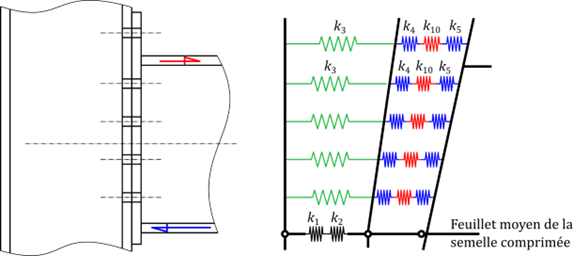
Une fois la rigidité de chaque composant caractérisée à l’aide du coefficient k_i adapté, la rigidité initiale en rotation S_j,ini de l’assemblage poutre-poteau peut être déterminée, sous réserve de procéder à quelques simplifications.

La première simplification consiste à regrouper les ressorts constituant chaque rangée de boulon en un seul ressort « efficace » pour la rangée, comme montré sur la figure suivante. Pour une rangée  donnée, le coefficient de rigidité efficace obtenu pour une association de ressorts disposés en série est calculé au moyen de l’expression suivante :

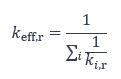
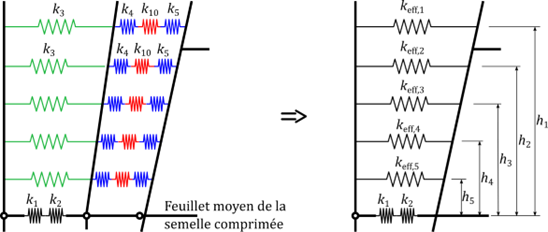
La seconde simplification correspond à la détermination d’un ressort « équivalent » représentant toute la zone tendue dans laquelle les ressorts associés à chaque rangée sont disposés en parallèle. Il est considéré que les sections droites restent droites et qu’elles tournent autour du centre de compression, positionné, par convention, au feuillet moyen de la semelle comprimée. Par rapport à ce point de référence, le ressort équivalent à la zone tendue est positionné à une distance z_eq définie comme suit :

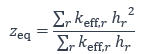
Le coefficient de rigidité équivalent à la zone tendue est ensuite calculé comme suit :

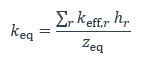
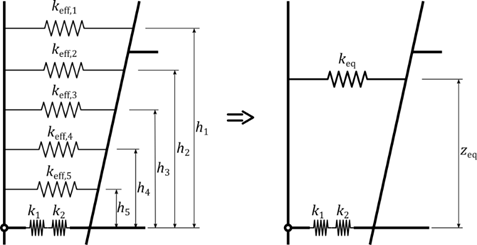
La rigidité initiale en rotation de l’assemblage poutre-poteau peut ensuite être déterminée par l’expression suivante :

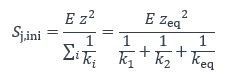
La rigidité initiale en rotation  s’exprime généralement en kN.m/rad. Elle représente le moment qu’il est nécessaire d’appliquer pour que l’assemblage se déforme d’un radian (quasiment 60°) si on suppose un comportement élastique et linéaire jusqu’à une telle déformation. Cela explique que la valeur obtenue dans ce système d’unité est usuellement supérieure de plusieurs ordres de grandeur au moment résistant de l’assemblage.

La démarche est similaire pour d’autres typologies d’assemblages en flexion comme la continuité poutre-poutre par platine d’about, par exemple.

Références

[1] NF EN 1993-1-8 (2005) : Eurocode 3 – Calcul des structures en acier. Partie 1-8 : Calcul des assemblages. AFNOR. Décembre 2005.

Télécharger le document

Anthony Rodier, chef du service formation, CTICM