Renforcement d’une poutre par un plat soudé – Exemples
Cet article présente deux exemples de justification de la résistance en flexion d’une poutre à section en I simplement fléchie, le premier consiste en un plat soudé sous la semelle inférieure et le second en un plat soudé sur la semelle supérieure. Les calculs sont effectués selon les règles de l’Eurocode 3 Partie 1-1.
Des informations sur le renforcement d’une poutre sont données dans l’article Métalétech « Renforcement d’une poutre par un plat soudé » [1].
Section sans renfort
Données de l’exemple
Considérons le cas d’une poutre de plancher sur appuis simples, reconstituée par soudage, en acier S355. Les dimensions de la section transversale sont :
- Semelles : 200 mm x 12 mm
- Âme : 556 mm x 8 mm
Les dimensions des cordons de soudure âme-semelles ne sont pas pris en compte dans les calculs.
La portée de la poutre est : L = 6,80 m
Les charges sont uniformément réparties sur toute la longueur de la poutre :
- Charges permanentes en place avant renforcement de la poutre : G0 = 12 kN/m
- Charges permanentes appliquées après renforcement : G1 = 16 kN/m
- Charges variables appliquées après renforcement de la poutre : Q = 50 kN/m
- Conformément à la norme [2], le coefficient partiel pour la résistance des sections est : gM0 = 1,0.
- Il est supposé que la poutre est maintenue latéralement sur toute sa longueur et ne présente pas de risque de déversement.
Moment de flexion maximal dans la poutre
Pour les vérifications vis-à-vis des états limites ultimes (ELU), la combinaison d’actions conduit à une charge égale à :
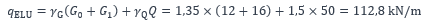
et à une valeur maximale du moment de flexion de :
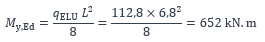
Classe de la section (sans renfort)
Pour la limite d’élasticité (nuance S355) ,

Élancement de la semelle comprimée :
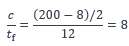
L’élancement de l’aile est inférieur à 10 ε = 8,1. La semelle est donc de Classe 2.
Élancement de l’âme :
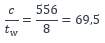
L’élancement de l’âme est supérieur à 83 ε = 67,2 et inférieur à 124 ε = 100,4. L’âme est de classe 3.
La section est de classe 3.
Vérification de la résistance en flexion (sans renfort)
La section étant de classe 3, il convient de se référer à la résistance élastique. Les propriétés élastiques de la section sont les suivantes :
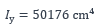
Moment d’inertie de flexion par rapport à l’axe fort de la section :
Module de résistance élastique par rapport à l’axe fort de la section :
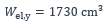
La contrainte normale maximale dans la section est :
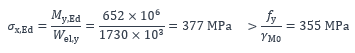
On constate que la contrainte maximale dépasse la limite d’élasticité de calcul. La section nécessite donc un renforcement.
Calcul de la section avec plat de renfort sous la semelle inférieure
Données complémentaires
Un plat 240 mm x 12 mm, en acier S355, est soudé sous la semelle inférieure de la poutre. Les propriétés de la section renforcée utiles pour le calcul sont :
- Position du centre de gravité par rapport à la face inférieure de la section de base :
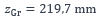
- Moment d’inertie de flexion par rapport à l’axe de forte inertie :
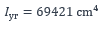

Il convient de calculer les contraintes normales dans la section, en tenant compte du phasage, pour les combinaisons ELU suivantes :

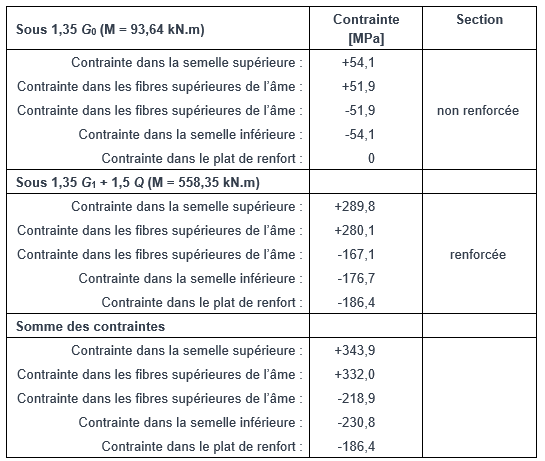
Sans donner tous les détails des calculs, les valeurs des contraintes normales sont données dans le tableau suivant en différents points sur la hauteur de la section. Les contraintes sont positives pour la compression et négatives pour la traction.
Classe de la section renforcée
La classe de la semelle supérieure comprimée n’est pas modifiée par la présence du plat de renfort. Elle est de classe 2.
La classe de l’âme doit être déterminée en tenant compte du plat de renfort et de la nouvelle répartition des contraintes normales. L’élancement de l’âme vaut :
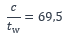
L’axe neutre élastique en flexion simple passe par le centre de gravité qui n’est plus situé à mi-hauteur de l’âme. Selon le tableau ci-dessus, le rapport des contraintes normales dans l’âme est :
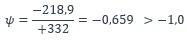
Il est à noter que la détermination de la classe de la section – entre classe 3 et classe 4 – doit être basée sur la répartition élastique des contraintes totales, tenant compte du phasage, comme illustré par cet exemple.
Selon le Tableau 5.2 de la NF EN 1993-1-1 [1], la limite d’élancement entre la classe 3 et la classe 4 est :
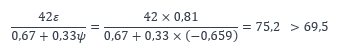
L’âme est de classe 3 et la section reste donc de classe 3 après renforcement.
Note : pour un plat de dimensions supérieures à celui choisi ici, le centre de gravité serait encore plus bas dans la section et l’âme pourrait être de classe 4.
Vérification de la résistance en flexion
La section étant de classe 3, il convient de vérifier que la contrainte normale maximale dans la section ne dépasse pas la limite d’élasticité de calcul :

Il est possible de calculer le taux de travail :
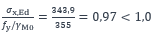
Le critère de résistance en flexion de la section est satisfait.
Calcul de la section avec plat de renfort sur la semelle supérieure
Données complémentaires
Un plat 160 mm x 12 mm, en acier S355, est soudé sur la semelle supérieure de la poutre.
Les propriétés de la section renforcée utiles pour le calcul sont :
- Aire de la section A=111,68 cm2
- Position du centre de gravité par rapport à la face inférieure de la section de base : zr,G=340,9 mm
- Moment d’inertie de flexion par rapport à l’axe fort : Ir,y =64112 cm4

Classe de la section renforcée
La classe de la semelle supérieure comprimée n’est pas modifiée par la présence du plat de renfort. Elle reste de classe 2.
La classe de l’âme doit être déterminée en tenant compte du plat de renfort et de la nouvelle répartition des contraintes normales. L’élancement de l’âme vaut :
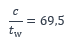
La partie comprimée de l’âme étant plus faible qu’en l’absence de renfort, une répartition plastique des contraintes normales est envisageable. Rappelons que l’axe neutre plastique divise la section en deux parties d’égales résistances. La limite d’élasticité étant identique en tout point de la section, il divise la section en deux parties d’aires égales.
L’aire de la semelle comprimée et de son renfort est inférieure à la moitié de l’aire totale de la section. L’axe neutre plastique est donc situé dans l’âme. En considérant que l’aire de la partie tendue est égale à la moitié de l’aire de la section, la position zANP de l’axe neutre plastique par rapport aux fibres inférieures s’exprime par :
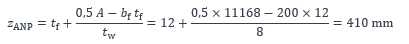
Le paramètre a qui représente la proportion comprimée de l’âme peut être calculé par :
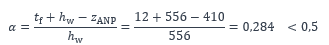
La limite d’élancement pour la classe 1 est :
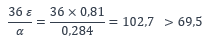
L’âme est de classe 1.
Le plat de renfort est uniformément comprimé sur toute sa largeur. Il peut être considéré comme une paroi maintenue sur ses bords. L’élancement du renfort est :

Le plat de renfort est de classe 1.
En conséquence, la semelle étant de classe 2, la section est de classe 2 et il est permis de vérifier sa résistance en flexion vis-à-vis de la résistance plastique.
Vérification de la résistance en flexion
Le module plastique de la section renforcée est : Wpl,y=2435 cm3. On en déduit la valeur du moment résistant :
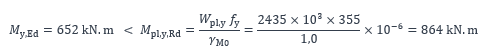
Le taux de travail est :

Le critère de résistance en flexion de la section est satisfait.
Conclusion
Une comparaison entre les résultats de ces exemples fait apparaître qu’il est plus efficace de renforcer la semelle comprimée que la semelle tendue, sous réserve que les conditions sur site le permettent.
Références
[1] BUREAU A., Renforcement d’une poutre par un plat soudé. Métalétech. Juin 2025.
[2] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
Alain Bureau, chef du service recherche construction métallique – CTICM