Vérification de la stabilité d’une poutre en flexion déviée

Cet article présente un exemple de vérification de la stabilité d’une poutre à section doublement symétrique en I sollicitée en flexion déviée (ou flexion biaxiale). La vérification est effectuée en suivant les prescriptions de la NF EN 1993-1-1 [1], en utilisant les formules d’interaction (§6.3.3) appliquées avec les facteurs d’interaction calculés selon l’Annexe B.

Données

L’exemple traité concerne une poutre HEB 280 de longueur L = 5 m présentée à la Figure 1. La poutre est soumise à un moment M_y appliqué dans son plan de forte inertie à une extrémité et à une charge uniformément répartie q_y appliquée perpendiculairement au plan de l’âme.

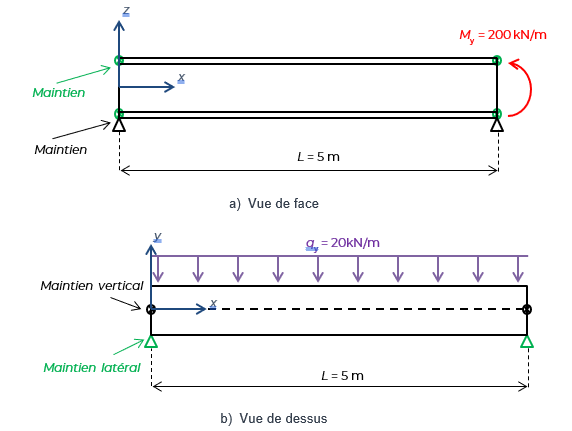
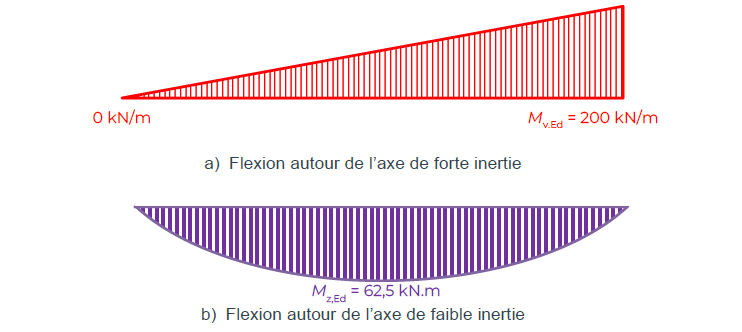
La poutre, bi-articulée, repose sur des appuis à fourche à ses extrémités : le déplacement le long de l’axe y et la rotation de torsion sont bloqués, alors que le gauchissement et la rotation autour de l’axe z sont libres [2]. Sous une combinaison d’actions ELU, la charge répartie et le moment d’extrémité prennent les valeurs indiquées à la Figure 1. Les moments fléchissants maximaux suivant les deux directions de flexion sont donc (voir Figure 2) :

Un acier de nuance S235 est utilisé. Étant donné que les épaisseurs des semelles et de l’âme sont inférieures à 40 mm, la limite d’élasticité est f_y = 235 MPa, conformément à la NF EN 1993-1-1 [1].

Par ailleurs, conformément à l’Annexe Nationale Française (NF EN 1993-1-1/NA [3]), les coefficients partiels utilisés sont : γ_M,0 = γ_M,1 = 1,0.

Résistance de la section transversale

Selon la référence [4], la section HEB 280 en acier S235 est de Classe 1 au sens de la NF EN 1993-1-1 [1] en flexion d’axe fort et en flexion d’axe faible. Par conséquent, la section est également de Classe 1 en flexion déviée. La résistance de la section transversale est alors vérifiée à partir des modules de résistance plastiques qui valent ici :

• W_pl,y = 1534 cm³ ;
• W_pl,z = 717,6 cm³.

Les valeurs de calcul des résistances de la section transversale à la flexion simple autour de l’axe y et autour de l’axe z sont :

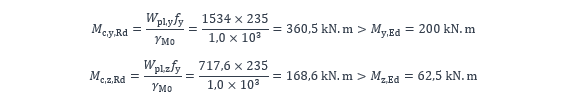
De plus, la résistance de la section transversale en tenant compte de la flexion déviée dans les deux plans est vérifiée en utilisant l’expression (6.41) de la NF EN 1993-1-1 [1]. Par simplification et se plaçant du côté de la sécurité, cette vérification est effectuée en prenant les valeurs maximales des moments de flexion bien qu’ils ne se trouvent pas dans la même section :

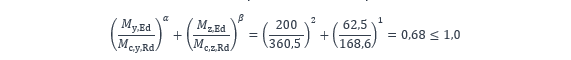
où α = 2 et β = 1 en l’absence d’effort normal pour les sections en I ou en H [1].

La résistance de la section au cisaillement doit être vérifiée, dans le plan de l’âme et dans le plan des semelles. Cette vérification est satisfaite mais n’est pas détaillée ici afin de limiter la longueur de cet article.

La résistance de la section est vérifiée.

Résistance au déversement

Moment critique de déversement

La NF EN 1993-1-1 [1] ne donne aucune expression analytique permettant de calculer le moment critique de déversement élastique M_cr de la poutre étudiée. Pour pallier l’absence de formulation dans la norme européenne, l’annexe nationale Française [3] fournit l’expression suivante :

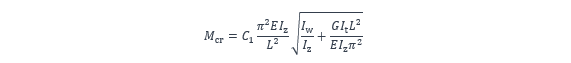
Les caractéristiques de la section utiles au calcul du moment critique sont :

• I_z = 6595 cm⁴,
• I_t = 143,7 cm⁴,
• I_w = 1130000 cm⁶.

Par ailleurs, le coefficient C₁ qui tient compte de la forme du moment de flexion d’axe fort prend la valeur 1,77 pour le diagramme de moment présenté à la Figure 2a). Le moment critique vaut donc :

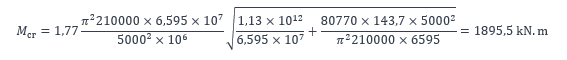
NOTE : La présence d’un moment de flexion d’axe faible n’a aucun effet sur le moment critique de déversement d’une poutre.

Vérification de la résistance au déversement

Le calcul de la résistance au déversement selon la NF EN 1993-1-1 [1] nécessite la détermination de l’élancement réduit pour le déversement :

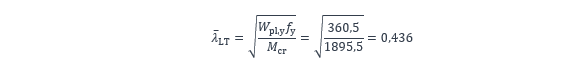
Conformément au Tableau 6.4 de la NF EN 1993-1-1 [1] pour un profilé laminé tel que h/b ≤ 2, la courbe a est choisie, soit : α_LT = 0,21. Le coefficient de réduction χ_LT est calculé comme suit :

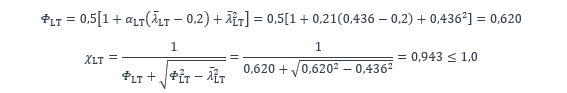
NOTE : Le coefficient de réduction est ici calculé selon le §6.3.2.2 de la NF EN 1993-1-1 [1], mais il est également possible de le calculer selon le §6.3.2.3 en tenant compte des règles de l’annexe nationale [3].

La résistance de calcul de la poutre au déversement est finalement obtenue à partir de l’expression suivante :

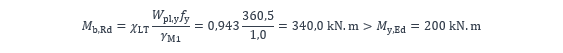
La résistance de la poutre au déversement est vérifiée.

Résistance de la stabilité en flexion déviée

Facteurs d’interaction

Les facteurs d’interaction k_ij sont déterminés en suivant les prescriptions de l’annexe B de la NF EN 1993-1-1 [1]. Cette méthode est appliquée conformément aux conditions fixées par l’Annexe Nationale en l’absence d’effort normal [3] :

• Les barres sont à section en I ou en H à semelles égales, ce qui est le cas pour un profilé HEB ;
• Les facteurs d’interaction sont déterminés en considérant les barres sensibles à la torsion.

NOTE : En présence d’effort normal, des conditions supplémentaires s’appliquent : la courbe a₀ ne doit pas être utilisée, et l’effort normal critique minimal doit correspondre au mode de flambement par flexion suivant l’une des deux directions principales.

En alternative, il est loisible de déterminer les facteurs k_ij à partir de l’annexe A de la NF EN 1993-1-1 [1].

Les valeurs des k_ij dépendent des facteurs de moment uniforme équivalents C_mi dont les valeurs sont obtenues d’après le Tableau B.3 [1] :

• C_my = C_mLT = 0,60 (diagramme de moment triangulaire dans le plan de forte inertie) ;
• C_mz = 0,95 (diagramme de moment parabolique dans le plan de faible inertie).

La poutre étudiée n’étant soumise à aucun effort normal (N_Ed = 0), les facteurs d’interaction sont obtenus à partir des expressions données dans le Tableau B.2 [1], conformément à l’annexe nationale française [3] :

En effet, l’élancement réduit pour le flambement d’axe faible est obtenu comme suit :

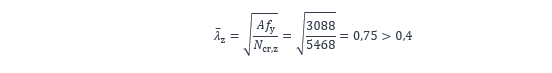
où :

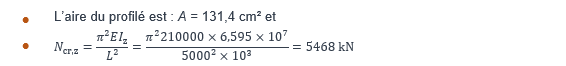
Vérification de l’interaction

Finalement, les formules d’interaction (6.61) et (6.62) de la NF EN 1993-1-1 [1] doivent être vérifiées. Seuls les termes de flexion sont retenus :

Les deux formules d’interaction en stabilité sont satisfaites. La résistance de la poutre est finalement vérifiée.

Références

[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pour les bâtiments. Octobre 2005.

[2] CTICM (2012) Déversement des poutres en acier.

[3] NF EN 1993-1-1/NA : Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pour les bâtiments – Annexe nationale à la NF EN 1993-1-1. Août 2013.

[4] Bureau, A. (2005) Classification des sections selon l’Eurocode 3 – Tableaux de classement des profilés laminés en I. Revue construction métallique, n°4, p. 59-73.

Télécharger le document

Maxime Lebastard, ingénieur de recherche, CTICM