Résistance en flexion d’une section de classe 3

Conformément à la NF EN 1993-1-1 [1], la résistance d’une section de classe 3 est basée sur une distribution élastique des contraintes normales dans la section, pour laquelle la contrainte maximale ne dépasse pas la limite d’élasticité de calcul. La norme offre cependant la possibilité de se référer à la résistance plastique pour une section dont la semelle comprimée est de classe 1 ou 2 et l’âme est de classe 3 en considérant des largeurs efficaces pour la partie comprimée de l’âme.

Cet article ne couvre que le cas d’une section en I doublement symétrique, de classe 3, en flexion simple par rapport à son axe de forte inertie, que la section soit laminée à chaud ou reconstituée par soudage.

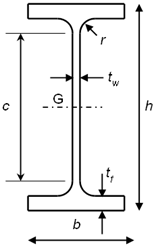
Pour une section reconstituée par soudage, il convient de prendre , où a est l’épaisseur de gorge des cordons de soudure d’angle.

Conditions d’élancement d’une section de classe 3

Une section en I à semelles égales, en flexion simple par rapport à son axe de forte inertie, est de classe 3 si au moins l’une des deux conditions suivantes est satisfaite (NF EN 1993-1-1, Tableau 5.2) :

• Condition d’élancement de la semelle uniformément comprimée

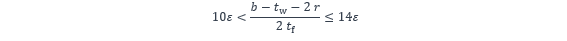
• Condition d’élancement de l’âme simplement fléchie

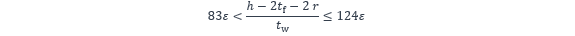
où

Résistance élastique

La condition de résistance élastique en flexion simple d’une section de classe 3, par rapport à son axe de forte inertie, peut s’exprimer de la façon suivante :

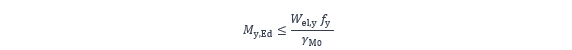
où :

M_y,Ed est le moment de flexion appliqué à la section ;

W_el,y est le module de résistance élastique de la section ;

γ_M0 est le coefficient partiel applicable à la résistance des sections : γ_M0 =1,0

Résistance plastique d’une section de classe 3

Il est toutefois permis d’utiliser le moment de résistance plastique de la section, en considérant des largeurs efficaces pour la zone comprimée de la partie droite de l’âme (voir la NF EN 1993-1-1, 6.2.2.4), si la semelle comprimée est de classe 1 ou 2. Cette condition peut s’exprimer par :

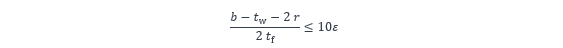
Il convient alors de calculer le moment de résistance plastique de la section avec les largeurs efficaces déterminées comme suit :

20 t_wε pour la partie comprimée adjacente à la semelle comprimée et,

20 t_wε pour la partie comprimée adjacente à l’axe neutre plastique (ANP).

La figure ci-dessous représente le diagramme des contraintes normales qui correspond à l’atteinte du moment de résistance plastique en tenant compte de ces largeurs efficaces. L’équilibre de la section en flexion simple conduit à considérer, pour une section doublement symétrique, une hauteur d’âme en traction égale à celle en compression, soit 40 t_wε .

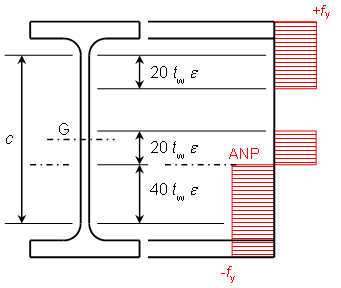
À partir de ce diagramme, il est possible d’exprimer un module plastique « efficace » de la section, que l’on choisit de noter ici W_pl,eff,y  :

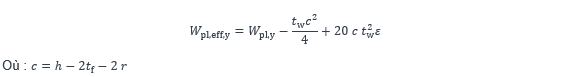
Cette formule n’est applicable qu’à une section avec une âme de classe 3 en flexion simple, c’est-à-dire :

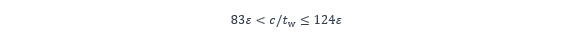
La résistance de calcul en flexion de la section est donc :

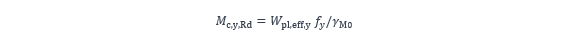
Lorsque l’élancement de l’âme est proche de la limite supérieure de la classe 2 (83ε ), la résistance en flexion ainsi calculée est proche du moment plastique de la section. En revanche, lorsque cet élancement est proche de la limite supérieure de la classe 3 (124ε ), elle tend vers la simple résistance élastique et le gain obtenu avec cette méthode est alors très faible. Cette méthode vise à réduire la discontinuité entre la classe 2 (résistance plastique) et la classe 3 (résistance élastique).

Exemple numérique

Prenons l’exemple d’un profilé reconstitué par soudage en acier S355, dont les dimensions sont indiquées sur le schéma ci-dessous. Cette section est soumise à un moment de flexion par rapport à son axe de forte inertie.

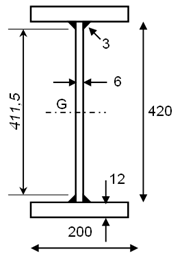
Module de résistance élastique :      W_el,y = 1176 cm³     

Module de résistance plastique :          W_pl,y = 1301 cm³   

Limite d’élasticité :                                f_y = 355 MPa, ε = 0,81

Classe de la section en flexion par rapport à l’axe de forte inertie

Classe de la semelle comprimée

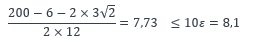
La semelle comprimée est de classe 2

Classe de l’âme

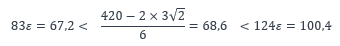
L’âme est de classe 3.

Résistance de la section en flexion

La section étant de classe 3, sa résistance élastique en flexion est :

Étant donné que la semelle comprimée est de classe 2 et que l’âme est de classe 3, le paragraphe 6.2.2.4 de la norme NF EN 1993-1-1 permet d’utiliser la résistance plastique de la section en considérant des largeurs efficaces pour la zone comprimée de l’âme comme présenté plus haut. Le module plastique efficace de la section est alors :

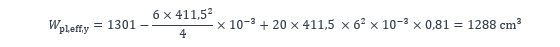
La résistance de calcul en flexion est finalement :

Pour cet exemple dans lequel l’élancement de l’âme est proche de la limite supérieure de la classe 2, le gain procuré par la méthode est d’environ 9,5%.

Références

[1]     NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.

Télécharger le document

Alain Bureau, chef du service recherche construction métallique, CTICM