Analyse globale d’un portique simple – Méthode EM
Cet article présente un exemple d’analyse globale d’un portique simple de bâtiment par la méthode dite « avec longueurs de flambement à nœuds déplaçables », selon les règles de l’Eurocode 3 Partie 1-1 [1] [2].
Introduction
Le lecteur peut se reporter à l’article Métalétech intitulé « Les méthodes d’analyse globale des ossatures de bâtiments » [4] afin d’avoir un aperçu de l’ensemble des méthodes d’analyse proposées par l’Eurocode 3 Partie 1-1 [1]. La méthode utilisée dans ce qui suit est la méthode EM. Les développements proposés dans cet article sont relatifs à la version actuelle de l’Eurocode 3, et resteront valables pour la version de deuxième génération.
Rappelons les règles relatives à l’application de cette méthode :
Conditions :
- Le coefficient d’amplification critique αcr doit être supérieur à 3,0.
Modalités d’application :
- Analyse élastique au premier ordre ;
- Aucune imperfection n’est à prendre en compte dans l’analyse globale ;
- À l’issue de l’analyse, il convient de vérifier la résistance des sections, ainsi que la résistance au flambement, dans le plan et hors plan, et au déversement des barres. Pour le flambement des poteaux dans le plan de la structure, il convient d’adopter une longueur de flambement pour un mode à nœuds déplaçables ;
- Pour la vérification des poutres (ou traverses) et des assemblages, la part de moment due à la déformation latérale de la structure doit être amplifiée par le coefficient kαi défini par :

- Où αcr est le coefficient d’amplification critique pour un mode d’instabilité globale.
Note 1 : pour une structure symétrique soumise à des charges verticales disposées symétriquement, les moments de déformation latérale sont les moments dus aux charges horizontales.
Note 2 : pour les poteaux, les effets de second ordre globaux sont indirectement pris en compte dans la vérification de la résistance au flambement, par l’utilisation de longueurs de flambement selon un mode à nœuds déplaçables dans le plan de la structure.
Pour plus d’explications sur l’analyse globale des structures en acier selon l’Eurocode 3, le lecteur peut également se reporter à la référence [3].
Description de l’exemple
Le portique étudié est constitué d’une seule nef et est entièrement réalisé en profilés laminés à chaud, de nuance d’acier S355.
La portée est de 16 m entre appuis et la hauteur des poteaux est de 5,80 m au point d’épure. La pente de la toiture est de 8,75%.
Note : Cet exemple est présenté avec quelques simplifications par rapport à la pratique, notamment en ne considérant qu’une combinaison d’actions, en négligeant la présence d’un renfort de jarret et en prenant les efforts aux points d’épure pour les vérifications.
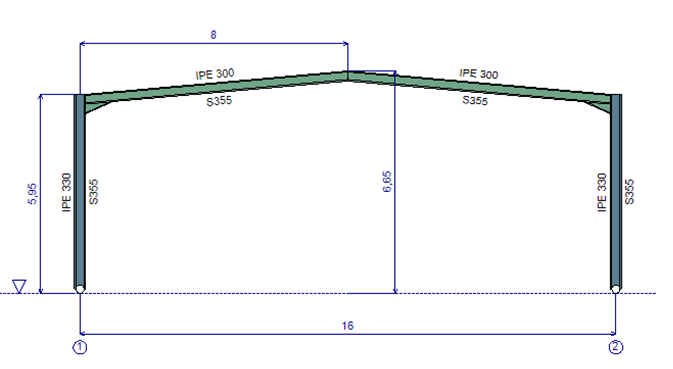
Maintiens latéraux vis-à-vis du flambement hors plan et du déversement
- Pour les poteaux, un maintien latéral est disposé à mi-hauteur ;
- Pour la traverse, les maintiens latéraux sont assurés par les pannes espacées de 2 m.
Note : pour les conditions de maintien, le lecteur peut se reporter à la fiche « Conditions de maintien vis-à-vis du déversement d’une poutre » [5].
Chargement étudié
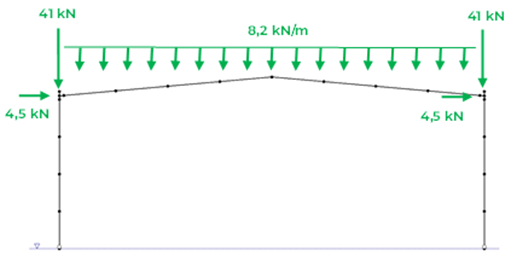
Le portique est étudié sous un seul chargement pour des vérifications vis-à-vis des états limites ultimes (ELU). Ce chargement est constitué des charges suivantes :
- une charge uniformément répartie sur la traverse : 8,2 kN/m
- une charge verticale en tête de chacun des deux poteaux : 41 kN
- une charge horizontale en tête de chacun des deux poteaux ; 4,5 kN
Ce chargement inclut notamment le poids propre de l’ossature.
Pour la combinaison étudiée, la valeur de calcul de la charge verticale totale est :

Détermination du coefficient d’amplification critique
Le coefficient d’amplification critique peut être déterminé par une analyse de flambement généralisé (recherche des modes propres d’instabilité). Pour des cas d’ossatures constituées de poteaux et de poutres, il peut être calculé simplement à partir de la rigidité latérale du portique (voir NF EN 1993-1-1:2004, 5.2.1(4)B). Pour cela, il est conseillé d’appliquer une charge fictive en tête des poteaux et d’effectuer une simple analyse élastique linéaire pour déterminer le déplacement horizontal qui en résulte. Voir l’article « Méthode pratique pour l’évaluation du coefficient d’amplification critique pour des portiques » [6].
Ici, le déplacement est celui obtenu sous le chargement horizontal effectivement appliqué en tête des poteaux, soit 35 mm. La rigidité latérale du portique est donc :

La charge verticale critique d’instabilité élastique est obtenue par :

Il est alors possible d’en déduire le coefficient d’amplification critique :

Le coefficient d’amplification critique étant inférieur à 10, il convient de prendre en compte les effets du second ordre dans l’analyse globale de la structure. En alternative, il est permis d’appliquer la méthode EM, dite « avec longueurs de flambement à nœuds déplaçables ». Pour cela, on vérifie : .
Note : un calcul de flambement généralisé donne un coefficient d’amplification critique égal à 6,63. Néanmoins la méthode précédente est satisfaisante pour évaluer la sensibilité du portique aux effets du second ordre globaux.
Analyse du portique au premier ordre (sans imperfection globale)
L’analyse élastique au premier ordre du portique conduit au diagramme du moment fléchissant, représenté à la figure ci-dessous.
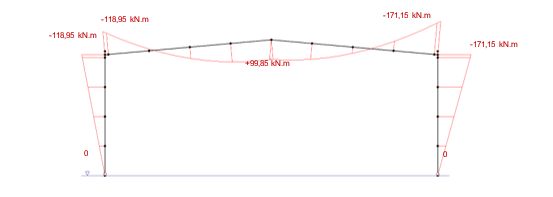
Les efforts dans la section la plus sollicitée du poteau sont (en valeur absolue) :
- Moment fléchissant maximal : My,Ed = 171,15 kN.m
- Effort axial maximal dans le poteau : NEd = 109,86 kN
Les efforts dans la section la plus sollicitée de la traverse sont (en valeur absolue) :
- Moment fléchissant maximal : My,Ed = 171,15 kN.m
- Effort axial maximal : NEd = 30,91 kN
Vérification de la résistance du poteau
A l’issue de l’analyse globale au premier ordre, la résistance au flambement et au déversement du poteau peut être vérifiée en utilisant directement les efforts indiqués précédemment, en adoptant comme longueur de flambement dans le plan du portique, celle pour un mode à nœuds déplaçables.
Les calculs détaillés de cette vérification sont donnés dans la fiche Métalétech « Vérification de la stabilité d’un poteau de portique » [7].
Vérification de la résistance de la traverse
En revanche, pour la vérification de la traverse et de l’assemblage à l’extrémité de la traverse, il convient de multiplier la part du moment fléchissant due à la déformation latérale (ici celle due aux charges horizontales) du portique par le coefficient :

Sous l’effet des charges horizontales, le moment fléchissant est :
Sous l’effet des charges verticales, le moment fléchissant est :
Pour la vérification du tronçon à l’extrémité de la traverse et de l’assemblage traverse sur poteau, le moment fléchissant à considérer est :
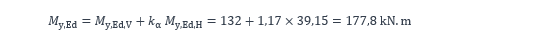
Références
[1] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[2] NF EN 1993-1-1/NA : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe nationale à la NF EN 1993-1-1. AFNOR. Mai 2007.
[3] Galéa, Y., Bureau, A., Guide Eurocode – Choix de l’analyse globale des ossatures en acier. CTICM-CSTB. Juillet 2011.
[4] Bureau, A., Les méthodes d’analyse globale des ossatures de bâtiments. Fiche Métalétech. Mai 2023.
[5] Bureau, A., Conditions de maintien vis-à-vis du déversement d’une poutre. Fiche Métalétech. Mai 2023.
[6] Bureau, A., Méthode pratique pour l’évaluation du coefficient d’amplification critique pour des portiques. Fiche Métalétech. Janvier 2020.
[7] Bureau, A., Vérification de la stabilité d’un poteau de portique. Fiche Métalétech. Janvier 2026. A paraître.
Alain Bureau, chef du service recherche construction métallique