Constructions mixtes – Calcul des poutres de planchers mixtes #1

Largeur participante de la dalle à prendre en compte pour le calcul des poutres mixtes

Introduction – Notions de base

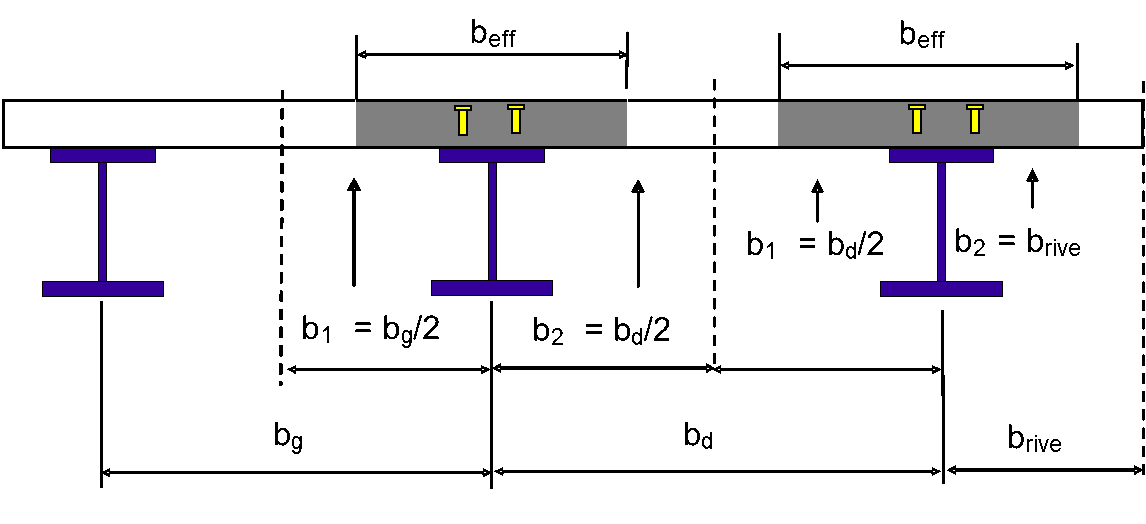
Dans un plancher mixte, le transfert de l’effort de cisaillement des connecteurs à la dalle ne mobilise pleinement celle-ci que si l’espacement bi entre poutres métalliques n’est pas trop grand (figure 1).

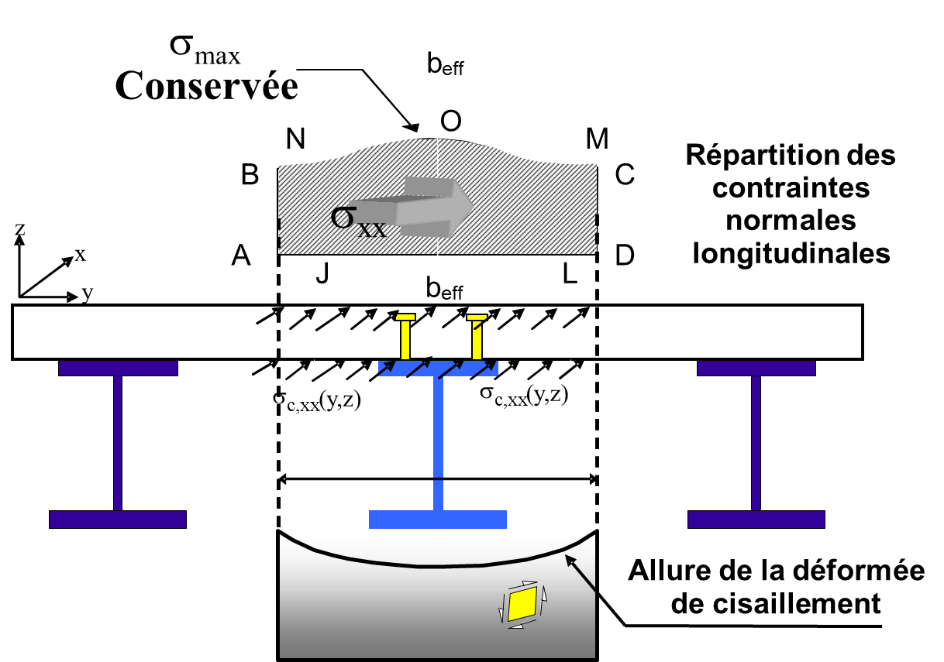
Cela signifie en particulier que les contraintes normales dans la dalle (par exemple au niveau de la face supérieure) ne sont pas distribuées uniformément : elles sont manifestement plus élevées au droit des poutres métalliques et plus faibles à mi-distance entre ces poutres; on parle souvent d’effet de « traînage par cisaillement » (figure 2).

Aussi, afin de pouvoir étudier le plancher comme un ensemble de poutres en T indépendantes, il est pratique d’introduire le concept de largeur participante b_eff de dalle revenant à fixer la largeur de celle-ci, pour chaque poutre métallique, qui contribue à la flexion générale du plancher avec l’hypothèse d’une distribution uniforme des contraintes normales sur cette largeur. Des travaux ont montré que la définition de b_eff dépendait, de manière complexe :

• de la présence ou non du glissement relatif entre la dalle et la poutrelle métallique (la largeur participante diminue en présence de glissement) ;
• de la présence de charges concentrées (la largeur participante est réduite au droit des charges concentrées) ;
• de l’épaisseur de la dalle (la largeur participante est plus importante pour les dalles épaisses) ;
• de l’espacement des poutres (plus l’espacement des poutres est faible plus la dalle est plus ou moins complètement mobilisée) ;
• de la distance entre les points de moment nul ou points d’inflexion dans le diagramme des moments fléchissants ;
• du type de comportement élastique ou plastique (le comportement plastique mobilise une largeur importante) ;
• etc.

Par la suite on parlera de largeur efficace qui est le terme adopté dans l’EN1994-1-1.

Calcul de la largeur efficace

C’est pourquoi, devant cette complexité, dans le domaine du bâtiment, la plupart des codes de dimensionnement proposent des formules simples qui se placent assez largement en sécurité. Dans l’EN 1994-1-1 il est proposé des expressions retenant uniquement trois facteurs : espacement des poutres, distance entre points de moment nul et espacement transversal des goujons qui est en pratique négligé.

Largeur efficace à mi-portée ou au niveau d’un appui intermédiaire

À mi-portée ou au niveau d’un appui intermédiaire, la largeur efficace totale b_eff peut être déterminée par l’expression :

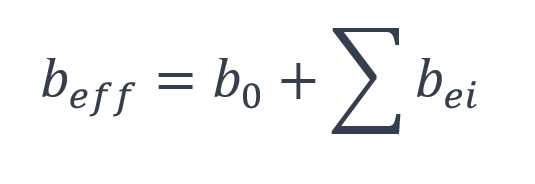
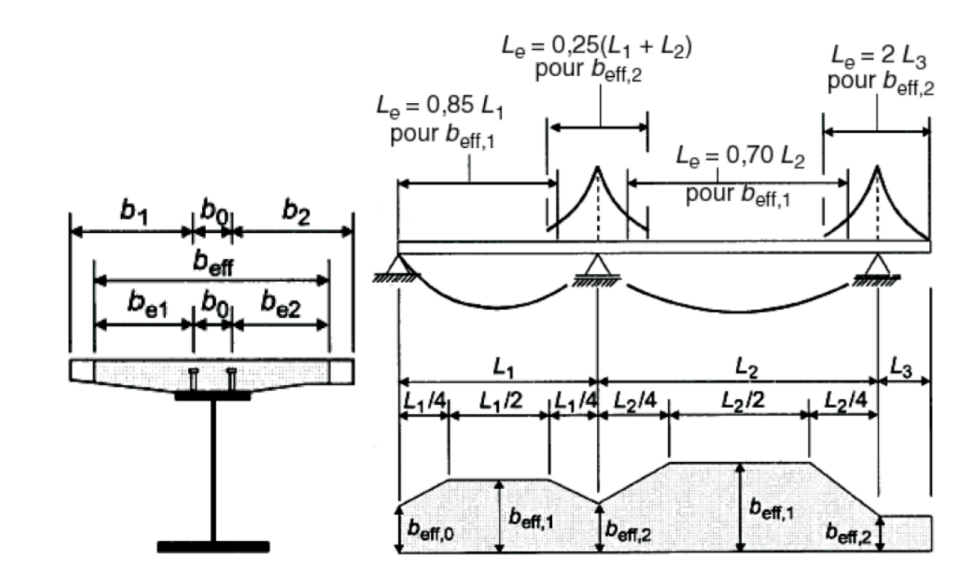
Par référence aux figures 1 et 3 :

• b₀ est l’entraxe transversal des connecteurs. En pratique on néglige b₀
• b_ei est la largeur efficace de la dalle en béton de chaque côté de l’âme, prise égale à L_e/8 sans être toutefois supérieure à la largeur géométrique b_i
• L_e est la distance approximative entre les points de moment fléchissant nul donnée à la figure 3

Largeur efficace au niveau d’un appui d’extrémité

La largeur efficace au niveau d’un appui d’extrémité est à déterminer par l’expression suivante :

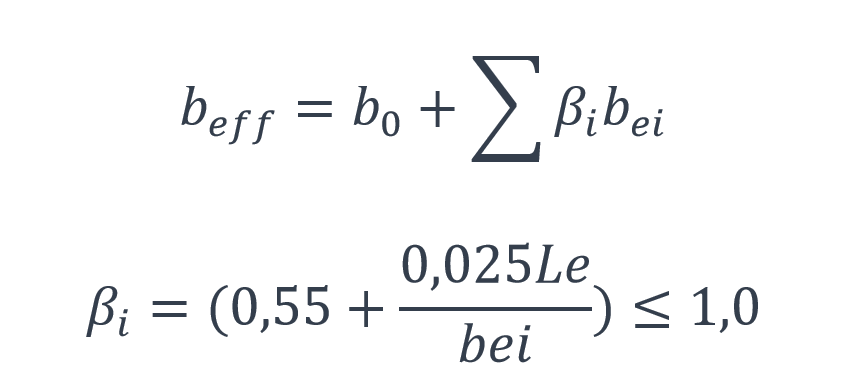
Dans ce cas, L_e est égal à 0,85 fois la longueur de la travée de rive et b_ei est à calculer en utilisant cette longueur.

Exemple 1 – Plancher mixte avec des poutres isostatiques

Pour un plancher mixte avec des poutres isostatiques d’une portée de 13,8 m, quelle est la largeur efficace à mi- portée pour la poutre intermédiaire et la poutre de rive ? On considère que b₀ = 0

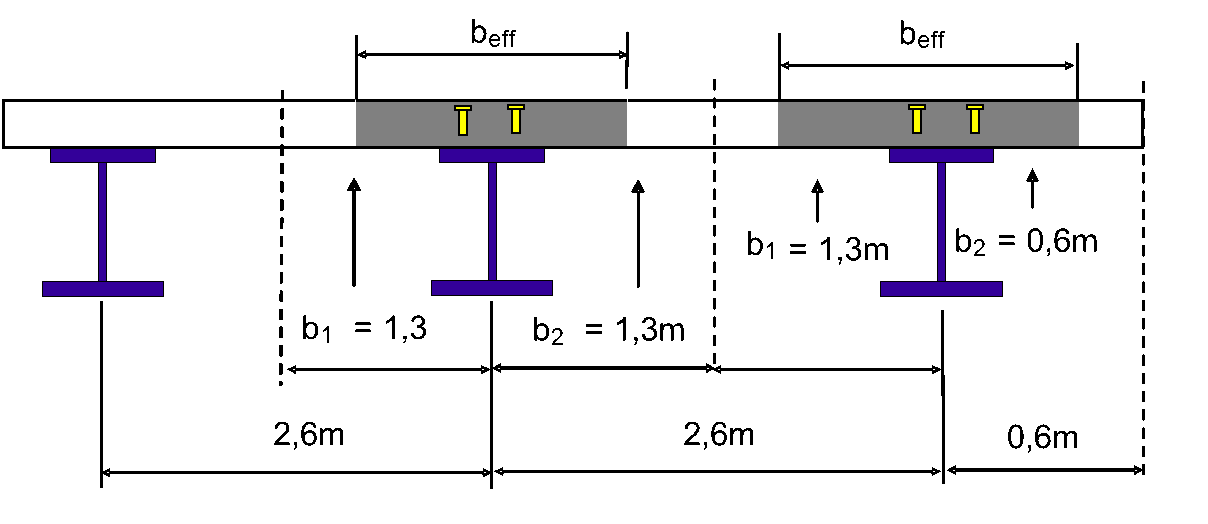
Poutre intermédiaire

b_eff à mi-portée = be1 + be2

b_e1 = b_e2 = min (13,8/8 ; 1,3m) = min (1,725 ; 1,3) = 1,3 m

b_eff à mi-portée = 1,3 x 2 = 2,6 m

Poutre de rive

b_eff à mi-portée = be1 + be2

b_e1 = min (13,8/8 ; 1,3) = min (1,725 ; 1,3) = 1,3 m

b_e2 = min (13,8/8 ; 0,6) = min (1,725 ; 0,6) = 0,6 m

b_eff à mi-portée = 1,3 + 0,6 = 1,9 m

Exemple 2 – Plancher mixte avec des poutres continues

On suppose que le plancher de l’exemple précédent est réalisé avec des poutres continues 2x10m

Quelle est la largeur efficace sur l’appui intermédiaire en supposant que b₀ = 0 ?

Pour l’appui intermédiaire L_e = 0,25x(10+10) = 5 m

Poutre intermédiaire

b_eff sur appui intermédiaire = b_e1 + b_e2

b_e1 = b_e2 = min (5/8 ; 1,3m) = min (0,625 ; 1,3) = 0,625 m

b_eff sur appui intermédiaire = 0,625 x 2 = 1,25 m

Poutre de rive

b_eff sur appui intermédaire = be1 + be2

b_e1 = min (5/8 ; 1,3) = min (0,625 ; 1,3) = 0,625 m

b_e2 = min (5/8 ; 0,6) = min (0,625 ; 0,6) = 0,6 m

b_eff sur appui intermédiaire = 0,625 + 0,6 = 1,225 m

Télécharger le document complet

Daniel Bitar, directeur du département études , CTICM