Valeurs précalculées de la température critique des éléments fléchis présentant un risque de déversement #10
Une démarche simple et pratique pour vérifier la résistance au feu des éléments de structures métalliques est celle basée sur des températures. Selon l’EN 1993-1-2 (novembre 2005) et son annexe nationale française (octobre 2007), la résistance au feu d’un élément de structure métallique peut être jugée satisfaite si l’échauffement θa de cet élément après la durée d’exposition au feu requise reste inférieure à sa température critique θa,cr.
Calcul de la température critique d’un élément fléchi avec déversement
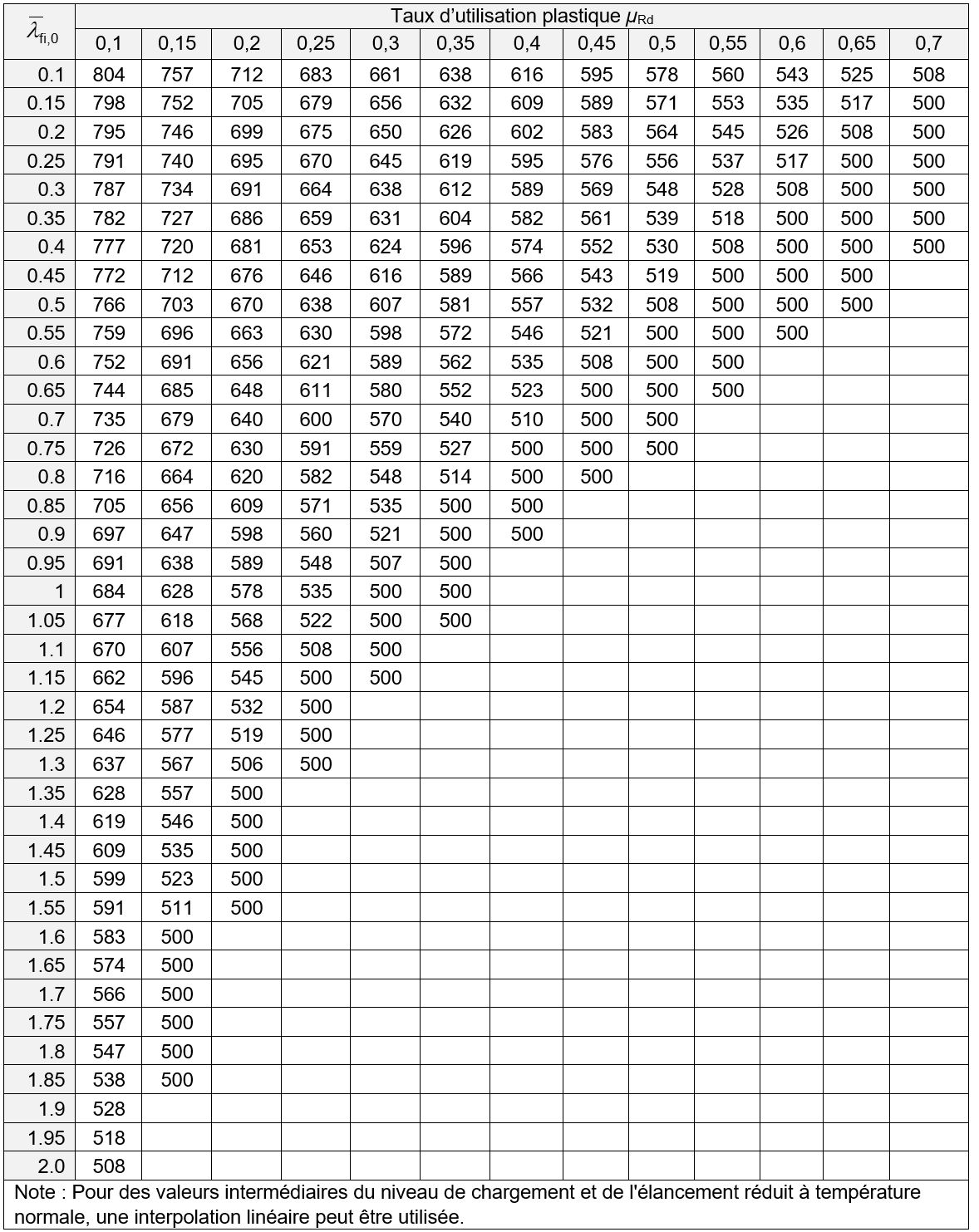
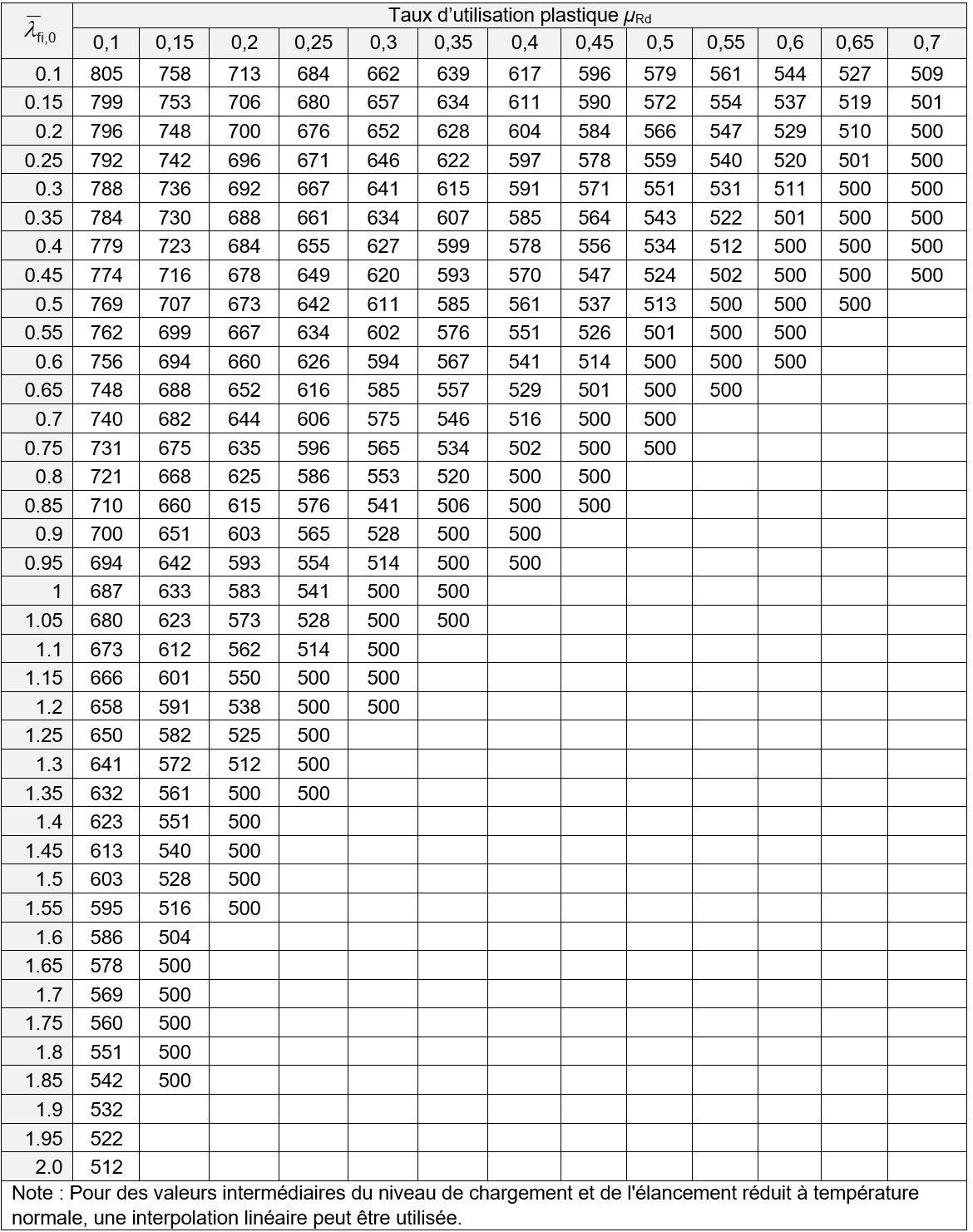
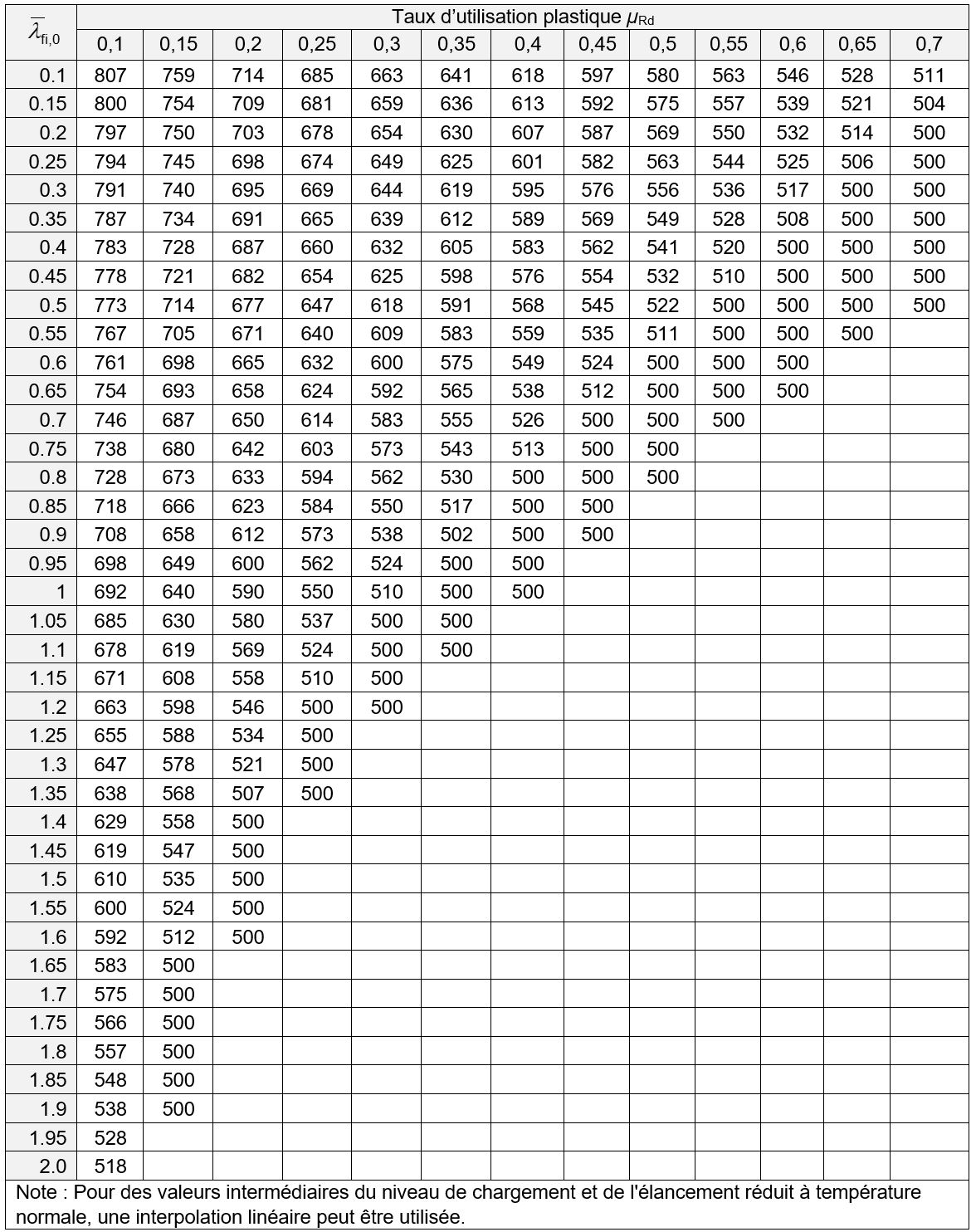
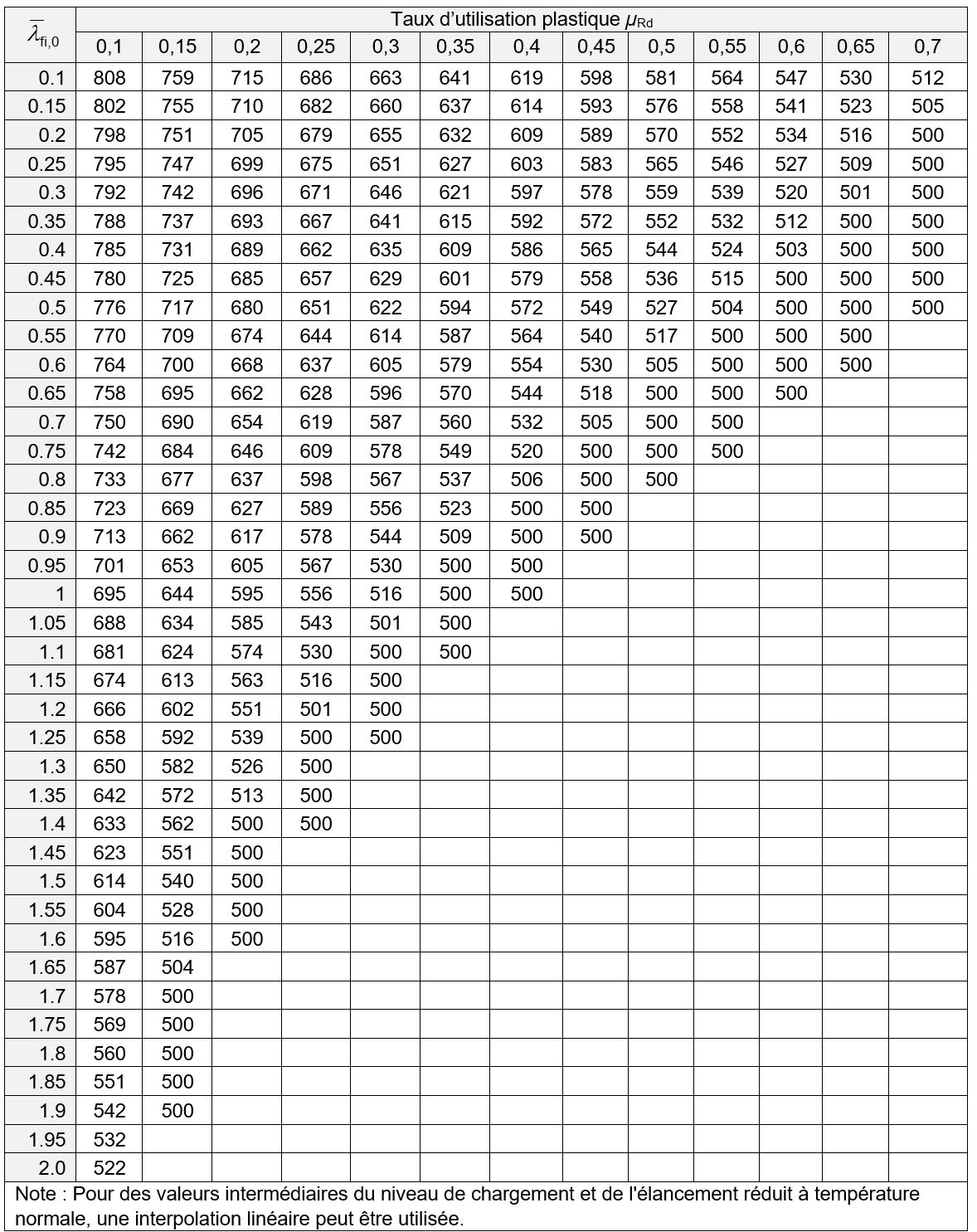
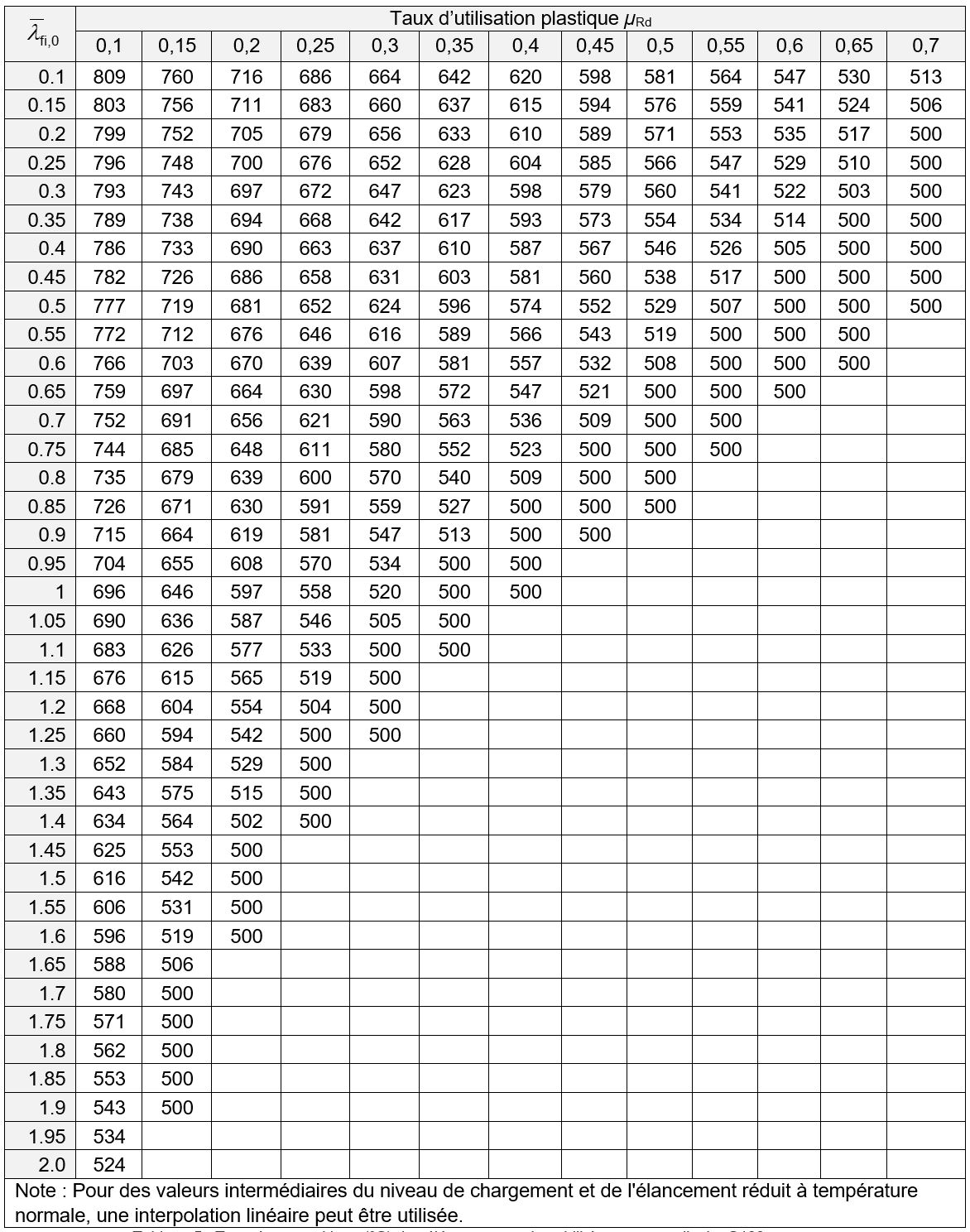
La température critique θa,cr des éléments de classe 1, 2 ou 3, fléchis présentant un risque de déversement peut être directement déterminée à partir des valeurs reportées dans les tableaux 1 à 5, en fonction de la nuance d’acier, de l’élancement réduit 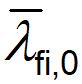
et du taux d’utilisation plastique µRd de l’élément.
Calcul du taux d’utilisation plastique
Le taux d’utilisation plastique µRd est donné par :

Où :
Wpl est le module de flexion plastiquede la section par rapport à l’axe approprié ;
Wel est le module de flexion élastiquede la section par rapport à l’axe approprié ;
fy est la valeur nominale de la limite d’élasticité de l’acier à froid.
Mfi,Ed est le moment fléchissant de calcul pour la situation d’incendie, déterminé conformément à la partie feu de l’EN 1991-1-2 (juillet 2003) et son annexe nationale française (février 2007).
Calcul de l’élancement réduit
L’élancement réduit 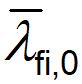 peut être calculé à partir des relations suivantes :
peut être calculé à partir des relations suivantes :

où Mcr est le moment critique pour le déversement élastique à température normale [N m], Wpl est le module de flexion plastiquede la section transversale [m3], Wel est le module de flexion élastiquede la section transversale [m3].
Le moment critique pour le déversement élastique à température normale peut être calculé à l’aide du logiciel LT-beam (en libre téléchargement sur le site du CTICM). Il peut également être déterminé selon l’annexe M de l’Annexe Nationale française de l’EN 1993-1-1 (août 2013) qui fournit une formulation approchée de Mcr pour les éléments ayant une section doublement symétrique, simplement fléchis et maintenues au déversement à leurs deux extrémités.
Dans le cas de conditions d’appui à fourches aux extrémités (rotation libre autour de l’axe z, rotation bloquée autour de l’axe x, déplacement bloqué suivant y et gauchissement libre), le moment critique pour le déversement élastique Mcr peut être calculé comme suit :
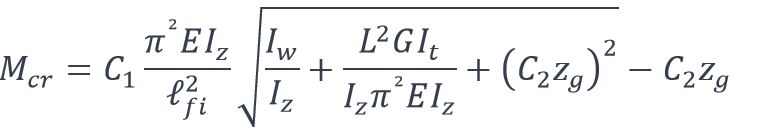
où C1 et C2 sont des coefficients dépendant des conditions de maintien et de chargement, E est le module d’élasticité, G est le module de cisaillement (G = 80 770 N/mm²), Iz est l’inertie de flexion par rapport à l’axe faible z, It est l’inertie de torsion, Iw est l’inertie de gauchissement zg est la distance entre le point d’application de la charge et le centre de gravité de la section transversale et est la longueur de déversement en situation d’incendie de l’élément considéré.
En règle générale, la longueur de déversement en situation d’incendie est considérée comme identique à celle retenue dans le dimensionnement à froid.
Pour une poutre soumise à une distribution uniforme de moments fléchissant (absence de charge transversale), on peut noter que C1=1 et C2 =0. Pour une poutre simplement appuyée et soumise à une charge uniforme, C1=1,13 et C2 =0,45. D’autres cas de chargement peuvent être trouvés dans l’Annexe M.
Christophe Renaud , directeur de projet de recherche – CTICM