Moment critique de déversement élastique de poutres uniformes à section mono-symétrique

La vérification vis-à-vis du déversement d’une poutre simplement fléchie selon l’Eurocode 3 Partie 1-1 [1] requiert la détermination de son moment critique de déversement élastique. L’annexe nationale [2] en donne une expression pour des sections doublement symétriques mais aucune expression n’est donnée pour les sections mono-symétriques. La référence [3] propose un modèle analytique qui est décrit ci-après.

Celui-ci concerne les poutres à section uniforme et symétrique par rapport au plan de flexion, reposant sur des appuis à fourche à leurs extrémités, le gauchissement et la rotation hors plan étant libres. Différents cas de chargement parmi les plus courants en pratique sont étudiés. Pour des cas plus complexes, il est conseillé de déterminer le moment critique de déversement à l’aide du logiciel LTBeamN [4].

Expression du moment critique

L’expression du moment critique de déversement élastique donnée ci-après s’applique dans le cadre des hypothèses suivantes :

• Poutre à section constante et symétrique par rapport au plan de flexion ;
• Poutre soumise à des moments aux extrémités ou à un chargement transversal ;
• Maintien latéral aux deux extrémités par des appuis à fourche, avec gauchissement libre ;
• Aucun maintien intermédiaire.

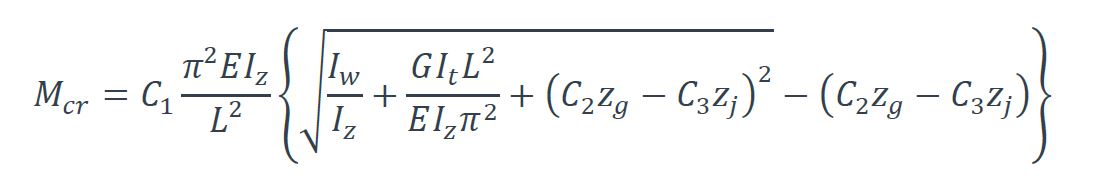
NOTE        Le terme « appui à fourche » désigne un maintien en déplacement latéral et en rotation autour de l’axe longitudinal de la poutre, la rotation hors du plan de sollicitation étant libre.

avec:

E       Module d’élasticité de l’acier ;

G       Module de cisaillement de l’acier ;

I_z        Inertie de flexion hors du plan de sollicitation de la section ;

I_w       Inertie de gauchissement de la section ;

I_t        Inertie de torsion de la section ;

L        Longueur du tronçon de poutre entre maintiens au déversement ;

C₁, C₂ et C₃    Coefficients dépendant de la forme du diagramme des moments ;

z_g       Distance entre le point d’application du chargement et le centre de cisaillement de la section ;

z_j        Facteur de Wagner, prenant en compte la mono-symétrie de la section.

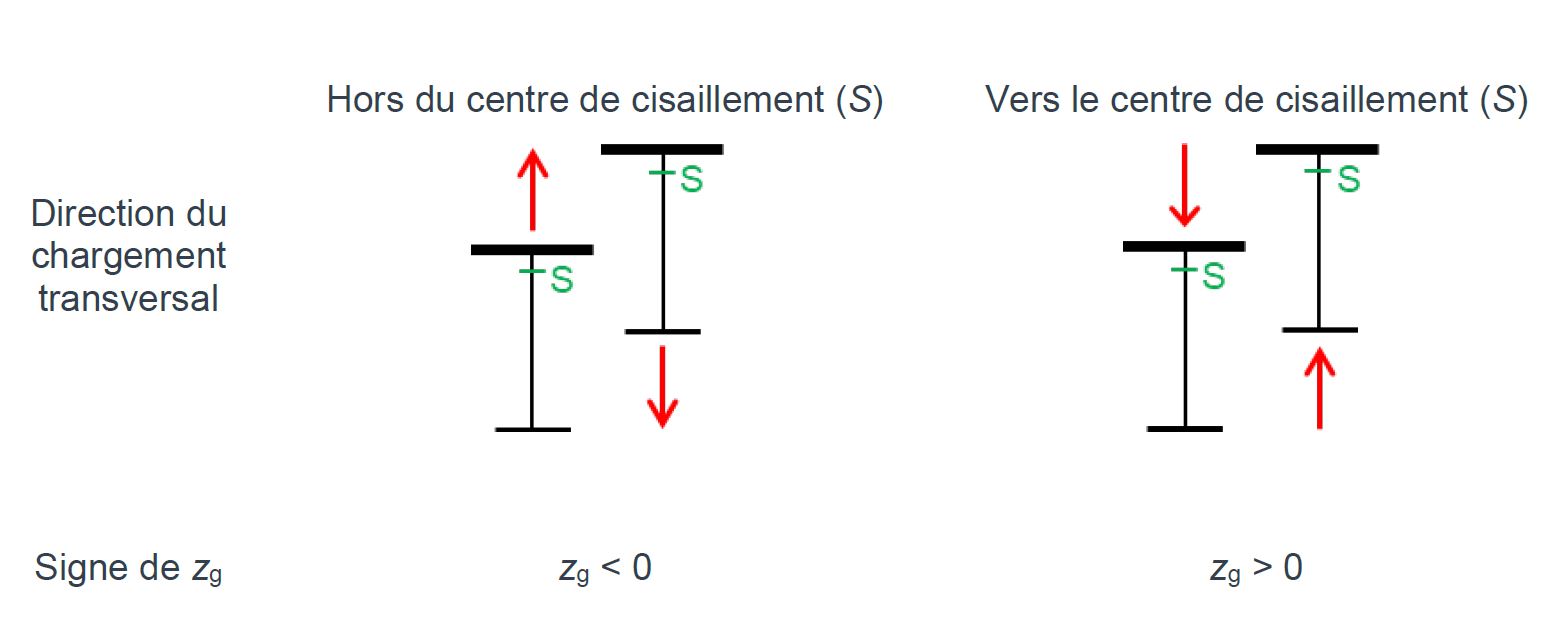
Un signe positif doit être assigné à z_g lorsque le chargement transversal a un effet déstabilisant, (dirigé vers le centre de cisaillement S). Pour un chargement transversal dirigé hors du centre de cisaillement, z_g est négatif (voir Figure 1).

En l’absence de chargement transversal entre les extrémités de la poutre (moment linéairement variable sur la longueur de la poutre) ou bien lorsque le chargement transversal est appliqué au centre de cisaillement, il convient de prendre : C₂z_g = 0.

Facteur de Wagner

Le facteur de Wagner est paramètre de calcul permettant de quantifier le « degré d’asymétrie » de la section transversale. Pour les sections en I à semelles inégales, il se détermine en utilisant l’expression suivante :

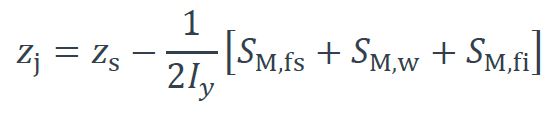
Où z_s est la coordonée du centre de cisaillement par rapport au centre de gravité de la section et avec :

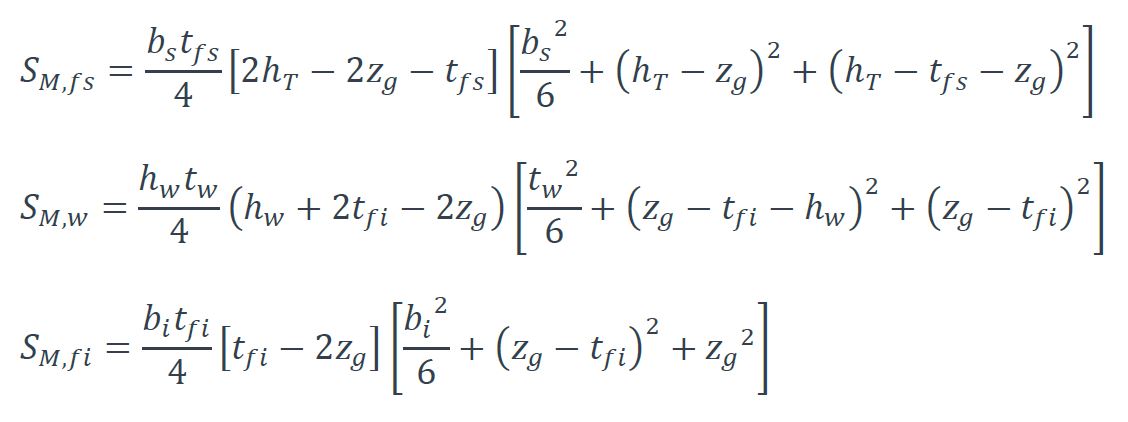
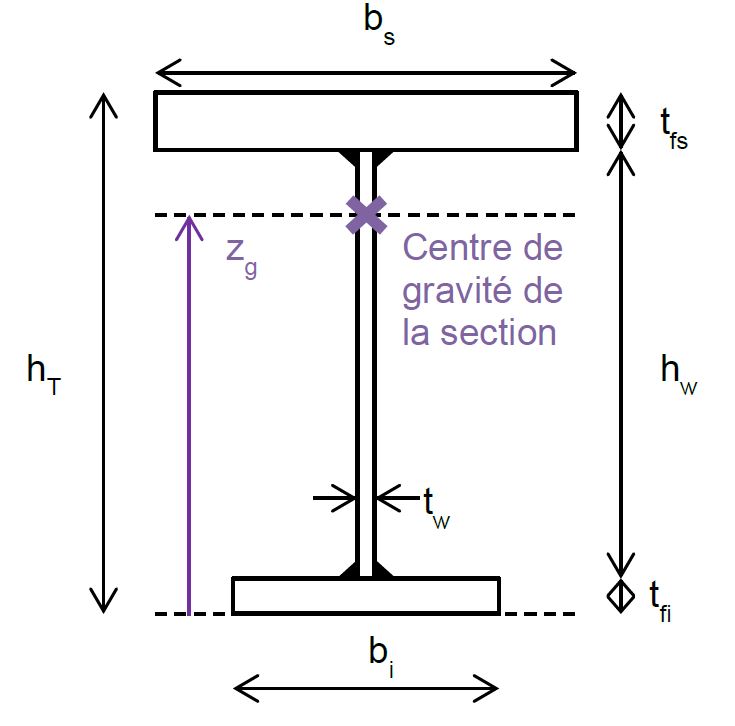
Les dimensions de la section transversale sont présentées à la Figure 2.

Dans le cas particulier des sections en I à semelles égales : z_j = 0.

La convention de signe pour le facteur de Wagner implique que z_j > 0 lorsque la semelle présentant la plus grande inertie hors du plan de flexion est comprimée au droit de la section située :

• à l’extrémité soumise au moment maximal pour une distribution du moment fléchissant variant linéairement de M à ψM (-1 ≤ ψ ≤ 1) ;
• à mi-portée dans le cas d’un chargement transversal.

Pour un diagramme de moment variant linéairement de +M à –M, le choix de la section d’extrémité à partir de laquelle le signe de z_j est déterminé est sans conséquence sur le résultat.

L’expression du facteur de Wagner donnée ci-dessus est également applicable aux rares cas de profilés laminés à section mono-symétrique, bien que les congés de raccordement âme-semelle soient négligés.

Coefficients C_i

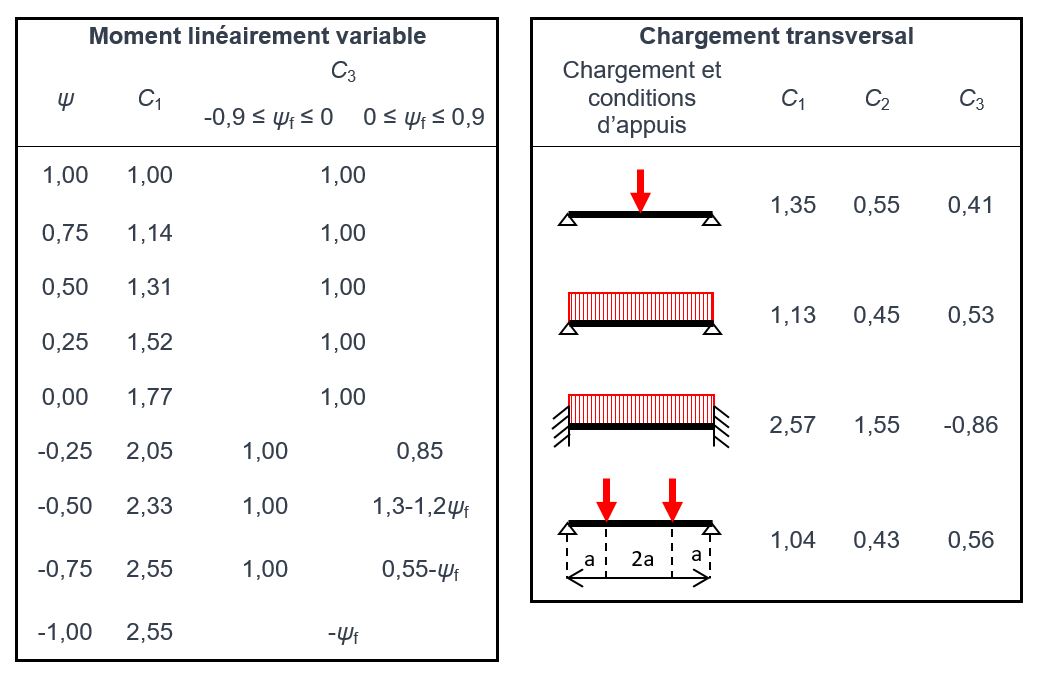
Les coefficients C₁, C₂ et C₃ dont dépend l’expression du moment critique sont présentés au Tableau 1.

Dans le cas d’un moment linéairement variable où ψ ≤ -0,50, le coefficient C₃ dépend du paramètre suivant :

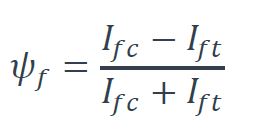
Où I_fc et I_ft représentent les inerties de flexion hors du plan de flexion de la semelle comprimée et de la semelle tendue, respectivement. La convention de signe pour ψ_f est identique à celle pour z_j : ces deux paramètres doivent avoir le même signe.

Références

[1] NF EN 1993-1-1 – Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pourles bâtiments. AFNOR, Octobre 2005.

[2] NF EN 1993-1-1/NA – Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe Nationale à la NF EN 1993-1-1. AFNOR, Mars 2007.

[3] Lebastard, M. ; Couchaux, M. ; Bureau, A. ; Hjiaj, M. (2022)  Déversement élastique de poutres en I à section mono-symétrique. Revue construction métallique n°1/2022, pp 3-15.

[4] CTICM. Logiciel LTBeamN v1.0.3, disponible en téléchargement libre sur le site du CTICM : www.cticm.com/logiciel/ltbeamn/

Télécharger le document

Maxime Lebastard, ingénieur de recherche – CTICM