Rupture d’un hauban / d’une suspente – Comment traiter ces situations accidentelles
Introduction
La norme française NF EN1993-1-11 – Avril 2007 [1] est en cours de révision et une nouvelle version est en cours de rédaction dans le cadre de la publication des Euronormes nouvelle génération.
La norme NF EN1993-1-11 – Avril 2007 comporte des erreurs au § 2.3.6 concernant le calcul de l’effet dynamique produit par la rupture d’un élément tendu. La norme NF EN 1993-1-11/NA – Décembre 2007 [2] corrige ces erreurs en indiquant que la formule du paragraphe 2.3.6 de cette norme donne des résultats erronés et propose une correction, mais sans donner à des ingénieurs non familiers avec le calcul des ponts haubanés et des ponts suspendus, les explications qui leur permettraient de comprendre le phénomène et d’appliquer correctement la règle.
La nouvelle version de la norme corrige cette erreur et propose une méthode supplémentaire, strictement équivalente, dite des forces opposées. Néanmoins, et pour les deux méthodes décrites dans le nouveau texte, des difficultés subsistes empêchant une application commode de la norme par les ingénieurs praticiens.
Cet article a pour but d’expliquer comment appliquer ces règles et comment traiter jusqu’au bout le cas de rupture d’un hauban ou d’une suspente dans les ponts haubanés et les ponts suspendus. La méthode des forces opposées est la plus simple à mettre en application dans les études d’exécution des ouvrages.
Tout en restant complètement conforme à la future version de la norme EN 1993-1-11 en cours de rédaction, le CTICM s’appuie sur la pratique française [3,4,5] pour asseoir ses préconisations.
Causes de rupture et coefficient de majoration dynamique k
Les principales causes de rupture des haubans et suspentes sont la corrosion et la rupture par fatigue produite par les frottements entre les fils des torons (le frottement entre et inter fils par fatigue). Mais aussi la rupture fragile, les chocs, l’incendie, etc. Il faut abandonner l’idée que la rupture d’un hauban ou d’une suspente est due à l’atteinte de sa résistance théorique.

L’effet dynamique de la rupture d’un élément tendu est difficile à quantifier avec précision, car il nécessite un grand nombre de données :
- la cause exacte de la rupture ;
- l’état de l’élément (câble, hauban, suspente) juste avant la rupture ;
- connaître ou faire des hypothèses plausibles sur la valeur des charges d’exploitation et de la température avant la rupture ;
- évaluer la durée de la rupture (temps en secondes ou fraction de seconde).
Une fois ces données définies, il y a lieu de procéder à un calcul dynamique transitoire, avec une fonction, par exemple, de type impulsion.
Cette démarche demande des temps d’étude importants, mais les règles simplificatrices de l’Eurocode permettent d’en faire l’économie.
Cependant, il faut choisir une valeur adaptée du coefficient de majoration dynamique, k. On peut se mettre du côté de la sécurité en adoptant une valeur de 2 qui est la plus grande valeur que fournit la mécanique. Mais, en se basant sur l’expérience acquise à travers les projets réalisés et les informations tirées de la littérature [3 à 7], le CTICM recommande les valeurs ci-dessous.
Pour des haubans MTP (multi torons parallèles), MFP (multi fils parallèles) et TMC (toron multi-couches) il est inconcevable que la totalité de la section soit rompue brutalement. En pratique, la rupture de quelques fils alerte le gestionnaire sur la nécessité du remplacement avant la rupture. Dans ces conditions le CTICM recommande l’utilisation d’un coefficient de majoration dynamique k égal à 1,5. De même, pour les câbles classiques à torons torsadés
Pour les suspentes en rond plein (ou barre) la rupture pouvant se faire d’un seul coup, notamment par fragilité ; nous gardons en mémoire l’effondrement du pont de Sully-sur-Loire et de la rupture des suspentes par une température de -20°C. Pour ces éléments le CTICM recommande l’utilisation d’un coefficient de majoration dynamique égal à 2.
Comment prendre en compte la rupture d’un hauban ou d’une suspente
Pour cette situation accidentelle, le CCTP du marché doit indiquer le nombre de haubans/suspentes sujet à rupture, ainsi que le coefficient de majoration dynamique à prendre en compte. Il n’est pas exclu d’imposer la rupture d’un nombre différent de haubans/suspentes d’une zone à l’autre pour les différentes zones de l’ouvrage, et des coefficients de majoration dynamique variable par zone, si cela se justifie.
En l’absence d’indication dans le CCTP du marché, la situation accidentelle « rupture de hauban ou suspente » est à étudier en considérant la rupture d’un seul hauban/suspente à la fois. Les coefficients de majoration donnés au paragraphe précédent de cet article peuvent être utilisés.
Le CTICM préconise l’application de la méthode des forces opposées, en conformité avec la future version de l’EN1993-1-11 et en conformité avec la pratique française [3,4,5] pour dimensionner des ouvrages vis-à-vis de la situation accidentelle de rupture d’un élément tendu.
Nous avons, par exemple, à calculer un pont haubané ou suspendu et nous avons à étudier le cas accidentel de la rupture des éléments tendus (câbles, haubans, suspentes).
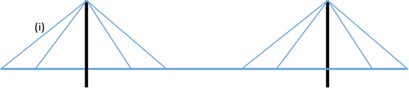
Pour chaque élément tendu (i) sujet à rupture (numéro i avec i allant de 1 à n où n est le nombre total d’éléments à prendre en compte) on détermine Ad,i les sollicitations accidentelles dues à la rupture de l’élément (i) en appliquant la démarche suivante :
1) Nous avons, par exemple, à calculer un pont haubané ou suspendu et nous avons à étudier le cas accidentel de rupture des éléments tendus (câbles, haubans, suspentes);
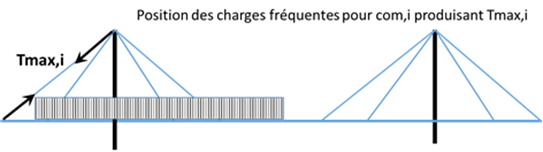
2) On supprime l’élément (i) et on applique une force égale et opposée (k-1)Tmax,i aux ancrages en présence des charges issues de la combinaison (com,i). Les efforts internes obtenus, y compris les nouvelles tensions dans les autres haubans ou suspentes, constituent les sollicitations de la situation accidentelle Ad,i. où k est le coefficient de majoration dynamique;
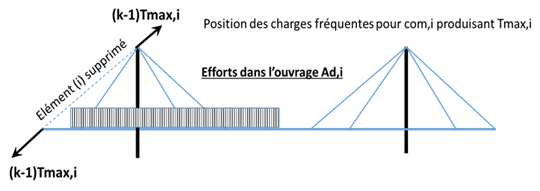
Ad,i : sollicitations dans l’ouvrage obtenues pour la combinaison accidentelle suite à la rupture du hauban i ;
3) On répète cette procédure afin d’obtenir les différentes Ad,i pour i=1 à n. n étant le nombre d’éléments sujet à rupture à étudier.
4) On établit les enveloppes min et max de ces sollicitations :
- Enveloppe max (Ad,1 ; Ad,2 ; Ad,3…Ad,i ; Ad,i+1…..Ad,n)
- Enveloppe min (Ad,1 ; Ad,2 ; Ad,3…Ad,i ; Ad,i+1…..Ad,n)
5) On procède aux vérifications à l’ELU de l’ouvrage en traitant ces enveloppes de la situation accidentelle de rupture des haubans/suspentes.
Pour éviter toute erreur d’interprétation, le calcul de l’effet de la rupture d’un hauban/suspente donné, ne donne pas une valeur réaliste des efforts lorsqu’on s’éloigne du hauban/suspente rompu. Seules les enveloppes donnent des résultats corrects à l’échelle de l’ensemble de l’ouvrage. Les deux méthodes approchées de l’Eurocode – qui sont équivalentes – assurent la sécurité de l’ouvrage, sans que les calculs menés sur un hauban/suspente donné soient représentatifs.
Erreur à éviter
Nous n’avons pas évoqué dans cet article la méthode d’évaluation de l’effet dynamique de la norme NF EN1993-1-11 – Avril 2007. Pour arriver à des sollicitations correctes dans l’ouvrage avec cette méthode actuelle, il convient de calculer l’effet dynamique par l’expression k(Ed2 – Ed1) et ajouter cet effet à la situation initiale Ed1 et non pas à Ed2. L’ajout de l’effet dynamique à Ed2 est une erreur contraire aux principes de la RDM et surtout au principe de St-Venant
Références
[1] NF EN 1993-1-11 : Eurocode 3 – Calcul des structures en acier. Partie 1-11 : Calcul des structures à câbles ou éléments tendus – AFNOR : avril 2007.
[2] NF EN 1993-1-11/NA : Eurocode 3 – Calcul des structures en acier. Partie 1-11 : Calcul des structures à câbles ou éléments tendus – Annexe nationale à la NF EN 1993-1-11 : 2007 – AFNOR : décembre 2007
[3] Guide méthodologique conception des ponts à haubans – Un savoir-faire français Cerema 2016
[4] Haubans – Recommandations de la commission interministérielle de la précontrainte – SETRA 2001
[5] D. BITAR – Conception avancé des ponts métalliques et mixtes – CHEM 2023
[6] L. DIENG et al. – Mécanisme de dégradation et moyens de protection des câbles – Mécanique & Industrie 10, 33-42 (2009)
[7] La résistance des structures aux actions accidentelles – Rapport d’étude 10/01/2007 INERIS-DRA-2007-N° 46055/77288 R N Formalisation du savoir et des outils dans le domaine des risques majeurs (DRA-35).
Remerciements
L’auteur tient à remercier Michel Virlogeux, consultant, pour la relecture de cet article.
Télécharger le document complet
Daniel Bitar, directeur du département études , CTICM