Résistance de calcul à température élevée des éléments métalliques #4 – Poutres simplement fléchies de classe 1,2, 3 sujettes au déversement

La partie 1-2 de l’Eurocode 3 et son annexe nationale française [1, 2], dédiés aux éléments de structure métallique, fournit différentes formules permettant de calculer la résistance au feu des éléments de structure métallique, tels que tirants, poutres et poteaux. Le présent article est consacré au calcul de la résistance au feu des poutres simplement fléchies de classe 1, 2 ou 3 sujettes au déversement.

Cet article est le quatrième d’une série de 7 consacrés à la résistance de calcul au feu :

1. Résistance de calcul à température élevée des éléments métalliques – Introduction
2. Résistance de calcul à température élevée des éléments métalliques – Éléments tendus ou axialement comprimés sans risque d’instabilité
3. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1, 2 ou 3 sans déversement
4. Résistance de calcul à température élevée des éléments métalliques – Poutres simplement fléchies de classe 1,2, 3 sujettes au déversement
5. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés axialement de classe 1, 2 et 3 sujets au flambement
6. Résistance de calcul à température élevée des éléments métalliques – Éléments comprimés et fléchis de classe 1, 2 ou 3
7. Résistance de calcul à température élevée des éléments métalliques – Assemblages

Calcul du moment résistant au déversement à température élevée

Pour les éléments fléchis sujets au déversement, le moment résistant de calcul au déversement en situation d’incendie à l’instant t est donné par la formule suivante :

Pour les éléments de classe 1 et 2 :

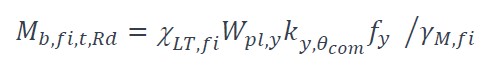
Pour les éléments de classe 3 :

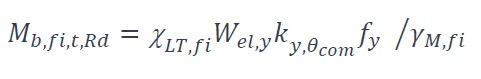
Où

χ _{T, i} est le facteur de réduction pour le déversement en situation d’incendie ;

_com est la température maximale dans la semelle comprimée. Cette température peut être supposée, en se plaçant du côté de la sécurité, égale à la température uniforme _a;

W_pl,y est le module de flexion plastique de la section transversale par rapport à l’axe fort ;

W_el,y est le module de flexion élastique de la section transversale par rapport à l’axe fort ;

f_y est la valeur nominale de la limite d’élasticité de l’acier à température normale ;

k_{y, com} est le facteur de réduction pour la limite d’élasticité de l’acier à la température _com  atteinte au temps t ;

γ_M,fi est le coefficient partiel de sécurité pour l’acier en situation d’incendie. Pour rappel, sa valeur est fixée à 1,0 dans l’annexe nationale française de l’EN 1993-1-2.

Calcul du facteur de réduction pour le déversement à température élevée

Le facteur de réduction pour le déversement χ _{T, i}  peut être calculé au moyen des formules suivantes :

Avec

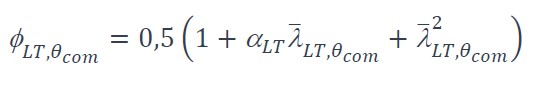
où il convient de déterminer le facteur d’imperfection pour le déversement  α_LT:

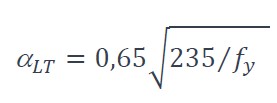
  où  f_y est la limite d’élasticité en N/mm²

et

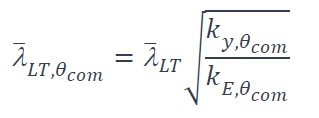
où

_{, om} est le facteur de réduction pour la pente du domaine élastique linéaire à la température maximale dans la semelle comprimée _om  atteinte au temps t,

et l’élancement réduit 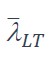 est donné par :

M_cr est le moment critique élastique de déversement, basé sur les propriétés de section transversale brute, tenant compte des conditions de chargement, de la distribution réelle des moments et des maintiens latéraux.

Pour les sections doublement symétriques et une distribution uniforme des moments fléchissants, le moment critique pour le déversement élastique à température normale M_cr peut être calculé à partir de la relation suivante :

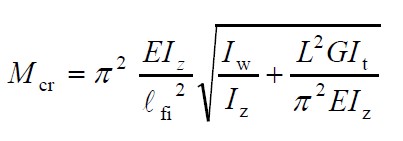
où E est le module d’élasticité, G le module de cisaillement, I_z l’inertie de flexion par rapport à l’axe faible z, I_t l’inertie de torsion, I_w l’inertie de gauchissement et l_fi la longueur de déversement en situation d’incendie de l’élément considéré.

En règle générale, la longueur l_fi de déversement  en situation d’incendie est considérée comme identique à celle retenue dans le dimensionnement à froid.

Références

[1] NF EN 1993-1-2 – Eurocode 3 – Calcul des structures en acier – Partie 1-2: Règles générales – Calcul du comportement au feu, avril 2005.

[2] NF EN 1993-1-2/NA – Eurocode 3 « Calcul des structures en acier » – Partie 1-2: Règles générales – Calcul du comportement au feu, annexe nationale à la NF EN 1993-1-2, octobre 2007.

Télécharger le document

Christophe Renaud, directeur de projet de recherche – CTICM