Exemple d’application- Résistance au flambement en compression simple

Cet article présente un exemple de calcul de la résistance au flambement d’une barre simplement comprimée selon l’Eurocode 3 Partie 1-1.

Données d’entrée

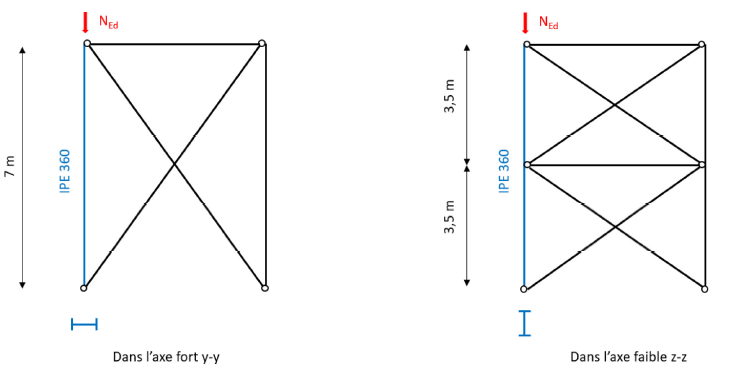
L’objet de cet exemple est de calculer la résistance au flambement du poteau simplement comprimé représenté à la Figure 1. La barre est maintenue vis-à-vis de l’instabilité :

• selon l’axe fort à ses deux extrémités ;
• selon l’axe faible à ses deux extrémités et au milieu de la barre.

Caractéristiques de la section

Le poteau est un profilé IPE 360 dont les caractéristiques sont :

• hauteur totale       h=360 mm
• épaisseur de l’âme t_w=8 mm
• largeur des semelles        b=170 mm
• épaisseur des semelles    t_f=12,7 mm
• rayon des congés r=18 mm
• aire de la section  A=72,7 cm²
• moment d’inertie de flexion autour de l’axe y-y   _y=16270 cm⁴
• moment d’inertie de flexion autour de l’axe z-z   _z=1043 cm⁴

Propriétés de l’acier

Le poteau est en acier de nuance S235. Les valeurs nominales de la limite d’élasticité sont déduites du Tableau 3.1 de la NF EN 1993-1-1 [1].

• limite d’élasticité :  f_y=235 MPa ( = 1)
• module de Young :  E=210000 MPa

Longueurs de flambement

Selon les conditions d’appui, les longueurs de flambement (voir référence [2]) :

• selon l’axe fort y-y :          L_cr,y=7 m
• selon l’axe faible z-z :       L_cr,z=3,5 m

Résistance au flambement

Classe de la section

La classe des semelles et celle de l’âme sont déterminées selon le Tableau 5.2 de la NF EN 1993-1-1 [1].

• semelles comprimées :

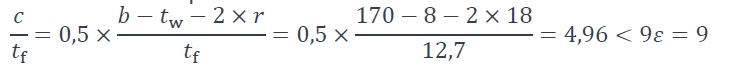
Les semelles comprimées sont de Classe 1

• âme comprimée :

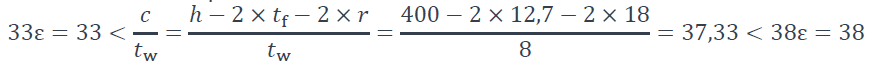
L’âme comprimée est de Classe 2

La section est de Classe 2.

Flambement selon l’axe fort y-y

L’effort axial critique de flambement est donné par l’expression suivante :

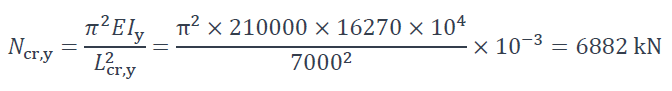
Élancement réduit selon §6.3.1.3 de la NF EN 1993-1-1 [1] :

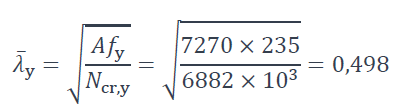
Courbe de flambement selon le Tableau 6.2 de la NF EN 1993-1-1 [1] : courbe a

Donc, le facteur d’imperfection   =0,21 pour courbe a (Tableau 6.1 de [1])

Le coefficient de réduction peut être directement obtenu à partir de la référence [3]. On donne cependant ci-après le calcul détaillé.

Le coefficient de réduction est calculé selon §6.3.1.2 de la NF EN 1993-1-1 [1] :

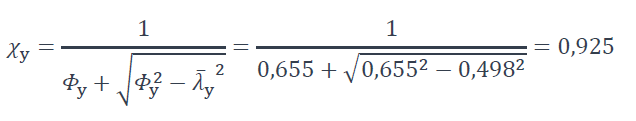
Où :

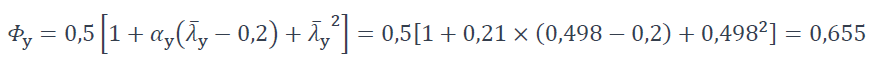
Résistance de calcul au flambement selon l’axe fort y-y (§6.3.1.1 de la NF EN 1993-1-1 [1]) :

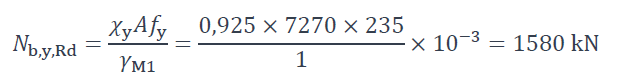
Flambement selon l’axe faible z-z

L’effort axial critique de flambement est donné par l’expression suivante :

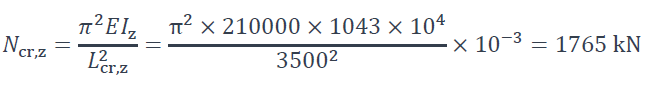
Élancement réduit selon §6.3.1.3 de la NF EN 1993-1-1 [1] :

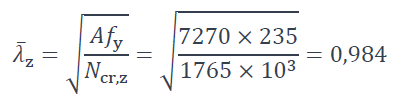
Courbe de flambement selon le Tableau 6.2 de la NF EN 1993-1-1 [1] : courbe b

Donc, le facteur d’imperfection =0,34  pour courbe b (Tableau 6.1 de [1])        

Le coefficient de réduction est calculé selon §6.3.1.2 de la NF EN 1993-1-1 [1] :

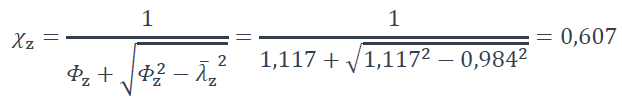
Où :

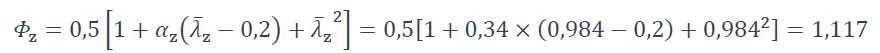
Résistance de calcul au flambement selon l’axe fort y-y (§6.3.1.1 de la NF EN 1993-1-1 [1]) :

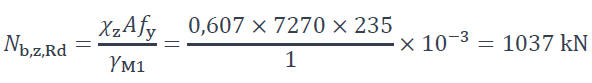
La résistance au flambement est donc :

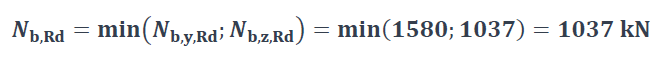
Références

[1]   NF EN 1993-1-1 – Eurocode 3 – Calcul des structures en acier – Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.

[2]   Phan, C.-V., Quelques cas simples de longueur de flambement d’une barre comprimée. Métalétech 2023, CTICM.

[3]   Bureau, A., Coefficient de réduction pour calculer la résistance au flambement l’Eurocode 3. Métalétech 2023. CTICM.

Télécharger le document

Cong Viet Phan, chef de projets recherche construction métallique – CTICM