Traînage de cisaillement

Le traînage de cisaillement est un phénomène affectant les semelles de grande largeur. La prise en compte de ses effets est traitée dans la norme NF EN 1993-1-5. Cette fiche présente le phénomène physique et les méthodes de calcul de la norme.

Le phénomène de traînage de cisaillement

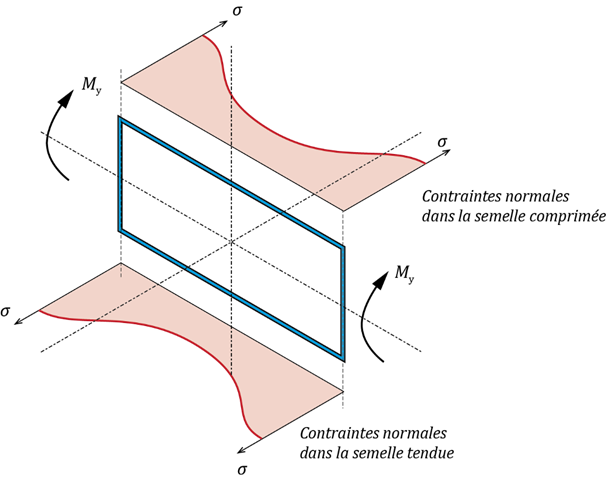
Le terme de traînage de cisaillement désigne le phénomène par lequel la répartition des contraintes normales dans les semelles d’une section fléchie par rapport à son axe de forte inertie n’est pas uniforme sur leur largeur. La contrainte est maximale au droit de la liaison âme-semelle, puis elle décroît progressivement à mesure que l’on s’éloigne de l’âme. Une autre façon de représenter le phénomène est de constater que, sous l’effet d’un moment de flexion, les sections planes ne sont plus réellement planes après la déformation, en raison de la largeur des semelles.

Le phénomène de traînage de cisaillement dépend de la portée de la poutre. Il est toutefois négligeable pour les semelles de largeur modérée, typiquement pour les sections en I ou H des profilés laminés courants. Dans ce cas, l’hypothèse de Navier-Bernoulli (les sections planes restent planes après déformation) peut être adoptée sans introduire d’erreur significative dans les calculs. Il en est de même pour son corollaire selon lequel les contraintes normales dans les semelles sont uniformes lorsque la section est soumise à un moment de flexion par rapport à son axe de grande inertie.

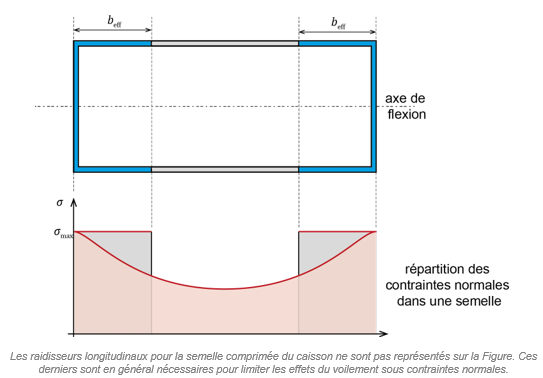
Le traînage de cisaillement doit être pris en compte pour les sections dont les semelles ont une largeur significative comparativement à la portée de l’élément. En pratique, cette configuration concerne essentiellement les ouvrages d’art, typiquement les ponts avec des sections en caisson (Figure 1).

Le traînage de cisaillement est un effet de distribution des contraintes normales à la section, indépendamment de tout phénomène d’instabilité. Il affecte aussi bien les semelles tendues que comprimées. Il influence la rigidité et la résistance de la section aux états limites ultimes.

Les méthodes de calcul relative au traînage de cisaillement sont intégrées dans le logiciel de calcul Z4. Ce dernier, d’utilisation gratuite, peut être téléchargé depuis le site internet du CTICM.

Concept de largeur efficace pour le traînage de cisaillement

La méthode des largeurs efficaces a été introduite afin de simplifier les calculs analytiques d’une section. Elle permet en effet de continuer d’effectuer les analyses élastiques (analyse globale ou analyse de section) avec l’hypothèse habituelle de Navier-Bernoulli. À cet effet, la section réelle est remplacée par une section équivalente, dont les semelles sont limitées par la largeur dite efficace, répondant aux deux conditions suivantes (Figure 2) :

• la contrainte maximale dans la semelle concernée reste identique à celle de la section réelle ;
• la résultante des contraintes normales reprises par la semelle reste identique à celle de la section réelle.

Le cas échéant, la largeur efficace pour le traînage de cisaillement doit être prise en compte pour l’analyse globale, les états limites de service, les états limites de fatigue et les états limites ultimes.

La largeur efficace relative au traînage de cisaillement ne doit pas être confondue avec la largeur efficace associée au voilement des parois. La norme NF EN 1993-1-5 distingue la largeur efficace^s pour le traînage de cisaillement et la largeur efficace^p pour le voilement (parois de classe 4). Pour une section affectée par les deux phénomènes, les deux réductions de largeur doivent être prises en compte (largeur efficace^s+p) dans les calculs. Alors que le traînage de cisaillement concerne les semelles tendues ou comprimées, le voilement est susceptible d’affecter toutes les parois totalement ou partiellement comprimées.

Largeur efficace due au traînage de cisaillement dans la NF EN 1993-1-5

Généralités

On adopte la méthode des largeurs efficaces lorsque l’étude de la structure n’intègre pas directement les effets du traînage de cisaillement. Dans le cas de l’analyse globale, cela concerne une modélisation d’une poutre par un élément filaire. C’est aussi le cas, pour l’analyse des sections, lorsque la répartition des contraintes dues aux sollicitations internes obtenues par l’analyse globale, est calculée à partir des propriétés de la section.

La norme NF EN 1993-1-5 [1] distingue deux modèles de largeur efficace de traînage de cisaillement : celui devant être appliqué pour l’analyse globale et celui pour l’analyse des sections.

Dans le cas d’une analyse par éléments finis où la structure étudiée est modélisée avec des éléments plaques, les effets du traînage de cisaillement sur la rigidité et sur la répartition des contraintes normales sont directement inclus dans le calcul. Il n’est alors pas nécessaire de prendre en compte les modèles de largeur efficace. Dans ce cas, les études par éléments finis doivent se conformer aux indications de l’Annexe C de la norme, en particulier en ce qui concerne les effets de voilement.

Largeur efficace de traînage de cisaillement pour l’analyse globale

Les clauses 2.2 (2) et (3) de la NF EN 1993-1-5 donnent les largeurs efficaces due au traînage de cisaillement devant être adoptées pour l’analyse globale. La largeur efficace d’une semelle est considérée comme constante sur toute la longueur d’une travée (ou d’une console). Elle est définie comme étant égale à la plus petite des valeurs de la largeur disponible et de L/8, où L représente la portée de la travée ou deux fois la longueur d’une console.

Largeur efficace de traînage de cisaillement pour l’analyse des sections

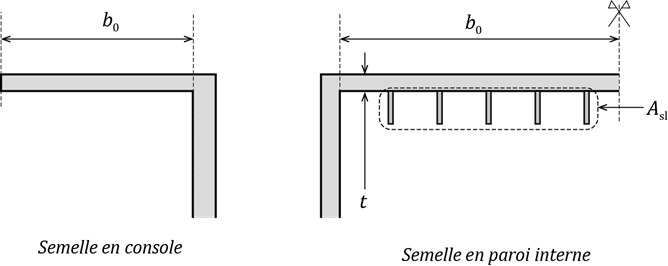
Dans l’analyse des sections, la clause 3.1 (1) de la NF EN 1993-1-5 précise que le traînage de cisaillement peut être négligé quand la condition suivante est vérifiée (Figure 3) :

où :      b₀ est la largeur de la partie en console (par exemple pour une section en I) ou la moitié de la largeur d’une paroi interne (par exemple pour une section en caisson) ;

L_e est la distance entre points de moments nuls dans le diagramme de moments.

Si la condition (1) n’est pas satisfaite, il est nécessaire d’adopter une largeur efficace pour le trainage de cisaillement dans la semelle concernée, quand le calcul de la section est effectué analytiquement. La norme NF EN 1993-1-5 distingue les options suivantes pour le calcul de cette largeur efficace :

• la méthode applicable pour un traînage purement élastique, devant être utilisée pour les états limites de service et de fatigue ;
• pour les états limites ultimes, la méthode élastique reste applicable. Une plastification limitée est toutefois généralement prise en compte, ce qui conduit à des largeurs efficaces plus importantes.

Largeur efficace pour le traînage de cisaillement élastique

La première méthode de calcul des largeurs efficaces pour le traînage de cisaillement suppose que la section reste dans le domaine élastique. Cette méthode est applicable pour les vérifications de tous les états limites. Dans ce cas, la largeur efficace de traînage de cisaillement est calculée de la manière suivante (cf. formule (3.1) dans la NF EN 1993-1-5) :

où β est un coefficient qu’il convient de calculer d’après le Tableau 1.

Le calcul de β dépend du paramètre k , qu’il convient de calculer par la formule suivante :

où :   α₀   est un coefficient représentant le taux de raidissage de la paroi. Il est calculé comme suit :

A_sl est l’aire de tous les raidisseurs longitudinaux présents sur la largeur b₀ (Figure 3).

Dans le cas d’une semelle non raidie, α₀.

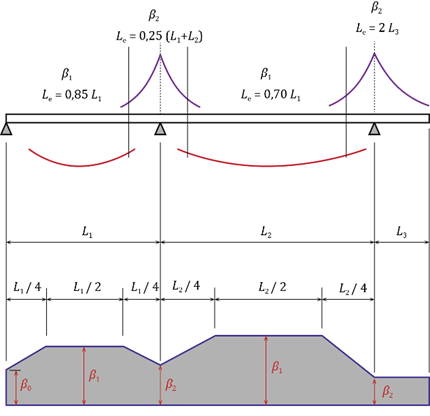
Le calcul de β dépend aussi de la forme du diagramme de moment : dans les zones sur appui intermédiaires où la pente du diagramme est forte, correspondant à un effort tranchant important, des largeurs efficaces plus faibles doivent être considérées. Inversement, en travée, la variation du moment est plus faible et des largeurs plus favorables sont possibles (Figure 4).

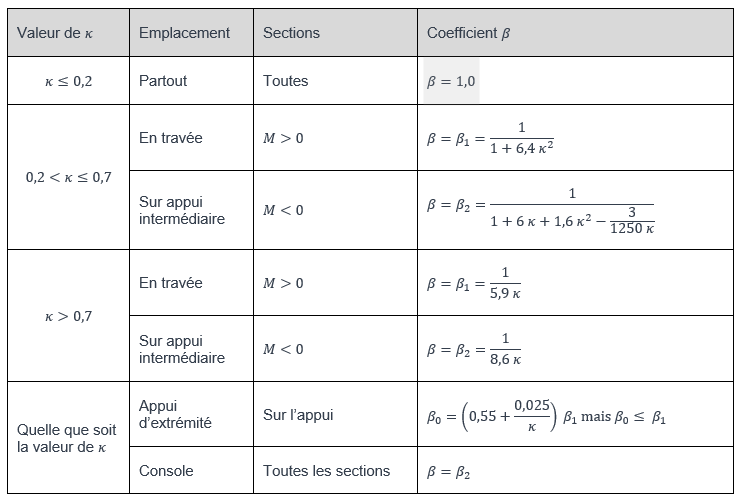
Le signe des moments de flexion dans le Tableau 1 correspond à un chargement gravitaire de la poutre.

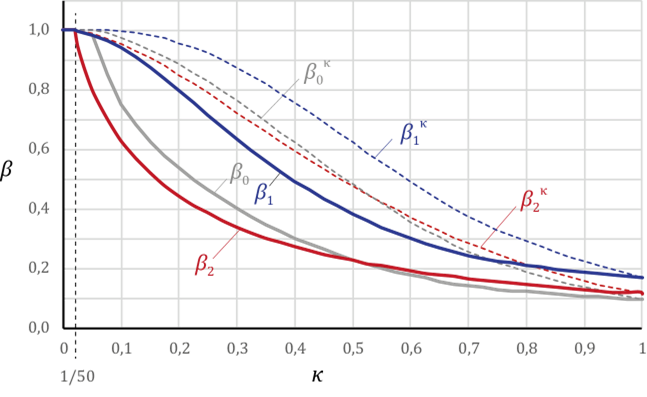
La répartition de la largeur efficace pour le traînage de cisaillement le long d’une poutre se fait suivant les indications de la Figure 5, laquelle indique aussi les valeurs de la distance L_e qu’il est possible d’adopter forfaitairement quand les travées internes adjacentes ne présentent pas un écart de longueur supérieur à 50% et quand la longueur d’une console n’excède pas la moitié de la portée de la travée adjacente.

Traînage de cisaillement aux états limites ultimes

Pour les états limites ultimes, une redistribution limitée des contraintes internes par une plastification locale est admise, conformément à la clause 3.3 (1) de l’annexe nationale [2]. Dans ce cadre, la partie efficace d’une semelle est obtenue par la relation suivante :

où A_f,eff est l’aire efficace de la semelle considérée prenant en compte le voilement. Pour une semelle comprimée :

 A_c,eff est l’aire efficace d’une semelle comprimée, tenant compte des effets de voilement, obtenue conformément à la clause 6 de la NF EN 1993-1-5.

Pour une semelle tendue, A_f,eff  est l’aire brute de la semelle.

Références

[1] NF EN 1993-1-5 : Eurocode 3 – Calcul des structures en acier – Partie 1.5 : Plaques planes – AFNOR – Mars 2007.

[2] NF EN 1993-1-5/NA : Eurocode 3 – Calcul des structures en acier – Partie 1.5 : Plaques planes – Annexe Nationale à la NF EN 1993-1-5 :2007 – AFNOR – Octobre 2007.

[3] Davaine L., Martin P-O : Vérification de la résistance au moment fléchissant d’une poutre raidie longitudinalement – Application de l’Eurocode 3 Partie 1-5. CTICM – Revue construction métallique n°3/2008.

[4] Beg D., Kuhlmann U., Davaine L., Braun B. : Design of plated structures. ECCS Eurocode Design Manuals – Ernst & Sohn. 2010.

[5] Johansson B., Maquoi R., Sedlacek G., Müller C., Beg D. : – Background documents in support to the implementation, harmonization and further development of the Eurocodes. Joint Report JRC-ECCS – Octobre 2007.

Télécharger le document

Pierre-Olivier Martin, chef du service DAL – CTICM