Principes de fiabilité dans les Eurocodes

La fiabilité des structures est essentielle pour garantir la sécurité des usagers et minimiser les risques économiques consécutifs à des désordres ou un effondrement d’une structure. Deux grandes approches permettent de traiter les incertitudes dans le dimensionnement : l’approche probabiliste, rigoureuse mais complexe, et l’approche semi-probabiliste, plus simple et largement adoptée dans les normes comme les Eurocodes [1].

Approche probabiliste de fiabilité

L’approche probabiliste repose sur le calcul direct de la probabilité de défaillance à partir de données statistiques. Elle permet de considérer explicitement les incertitudes sur les actions, les résistances, les géométries et les modèles de calcul :

En pratique, cette approche n’est jamais utilisée, car le calcul de P_f  peut s’avérer très complexe.

Approche semi-probabiliste de fiabilité

Pour simplifier l’application des principes de fiabilité, les Eurocodes adoptent une approche semi-probabiliste. Elle repose sur l’utilisation de coefficients partiels appliqués aux actions et aux résistances, selon le schéma de vérification suivant :

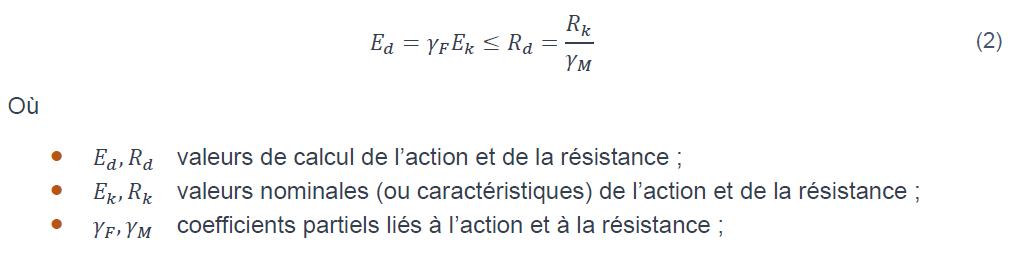
Les coefficients partiels  γ_F et  γ_F ont été déterminés à l’aide de méthodes probabilistes basées sur des données statistiques, afin de garantir un niveau de fiabilité cible sans avoir recours à un calcul probabiliste complet. Les valeurs sont données dans les différentes parties de l’Eurocode.

Note : Lorsque la valeur de calcul de l’effet des actions est égale à la valeur de calcul de la résistance, la probabilité de ruine est théoriquement celle qui est admise par la norme. Dans ce cas, le dimensionnement est optimal.

La calibration de ces coefficients repose sur la notion de marge de sécurité :

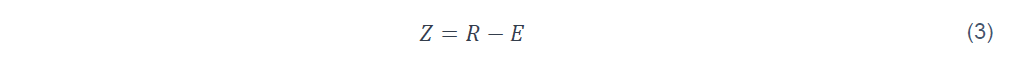
Où R et E sont respectivement les variables aléatoires associés à la résistance et à l’effet des actions.

Dans un cas simple, on suppose que les variables aléatoires R et E sont indépendantes et suivent des lois normales.

Alors, la variable Z suit également une loi normale, dont la moyenne et l’écart type s’expriment classiquement comme suit :

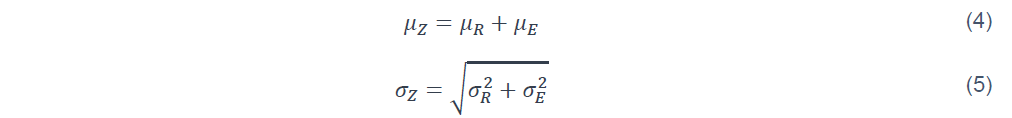
La probabilité de défaillance devient alors :

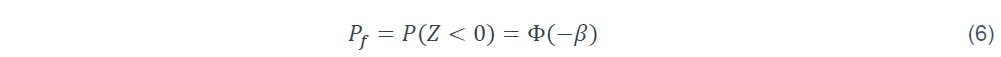
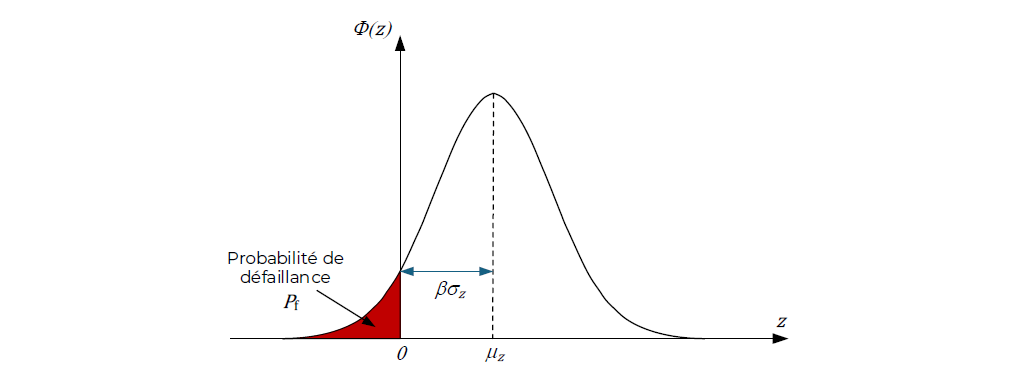
Où ϕ est la fonction de répartition d’une loi normale standard. Cette équation fournit une relation directe entre la probabilité de défaillance  P_f et l’indice de fiabilité β . Ce dernier quantifie la distance entre la moyenne de la marge de sécurité μ_Z et le point de défaillance Z=0, exprimée en nombre d’écarts types  σ_Z (voir Figure 1) :

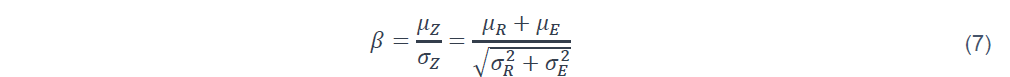
Plus l’indice β est grand, plus la structure est fiable, car la probabilité de défaillance P_f devient plus faible.

Note : en pratique, les variables n’ont pas toutes une distribution normale. Par exemple, une loi de distribution log-normale est généralement retenue pour la limite d’élasticité de l’acier. Des méthodes de calibration appropriées doivent alors être utilisées pour déterminer les coefficients partiels.

Il est possible de donner une interprétation graphique de l’indice de fiabilité β dans les coordonnées réduites (voir la Figure 2), définies par :

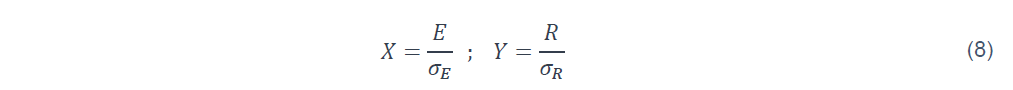
La droite d’état limite R-E=0 dans les coordonnées réduites s’écrit :

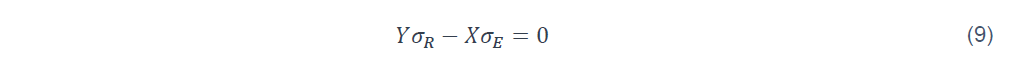
Cette droite coupe la densité jointe de probabilité f_x,y(x,y), créant le cercle de ligne de niveau circulaire dont le centre est défini par :

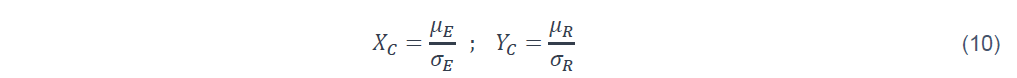
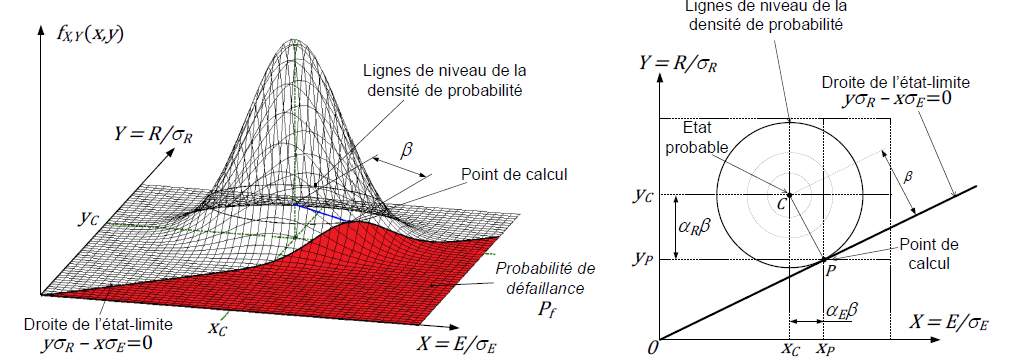
L’indice de fiabilité β correspond à la distance minimale entre le centre du cercle et le point de calcul P sur la droite d’état limite. Ce dernier représente le point de défaillance le plus probable, avec la probabilité acceptée P_f. Dans l’espace des variables X et Y , les coordonnées du point de calcul P sont :

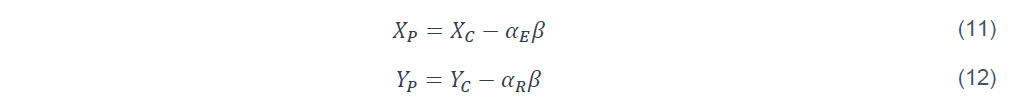
Dans l’espace des variables E et R, le point de calcul a pour coordonnées R_d et E_d :

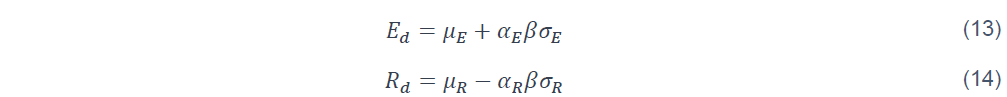
Les coefficients de sensibilité α_E et α_R  sont données par

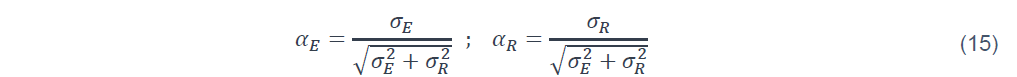
E_d et R_d sont les valeurs de calcul de l’effet des actions et de la résistance, respectivement. Ces valeurs sont utilisées en pratique par le projeteur et sont calculées par des méthodes données dans l’Eurocode. Dans le cadre semi-probabiliste, elles dépendent des paramètres (moyenne et écart type) des lois de distribution qui peuvent être estimés au préalable par l’exploitation de données statistiques. Cependant, comme montrée dans les équations (11), (13) et (15), la valeur de calcul de la résistance dépend de l’écart type de la sollicitation par le biais du coefficient de sensibilité α_R . De même, la valeur de calcul de l’effet des actions dépend de l’écart type de la résistance. Dans l’Eurocode, les valeurs suivantes de ces coefficients ont été fixées arbitrairement :

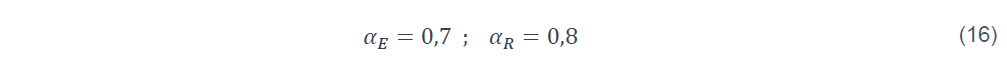
Donc, les coefficients partiels pour la résistance et l’effet des actions dans l’équation (2) peuvent être déterminés par :

Les valeurs des coefficients partiels de l’Eurocode ont été établies pour un indice de fiabilité β pris égal à 3,8 pour les états limites ultimes.

Références

[1]     NF EN 1990 : Eurocodes structuraux – Bases de calcul des structures. AFNOR, mars 2003.

[2]     Calgaro J.-A. : Éléments de fiabilité des constructions – Introduction aux eurocodes, Éditions du Moniteur, 2016.

[3]     Ducloux H. : Étude de la fiabilité structurale des pylônes treillis de lignes électriques aériennes soumises au vent. Revue construction métallique 2-2020, p. 4-14.

Télécharger le document

Piseth HENG, chef de projet recherche, CTICM