Poutres de chariots palans monorails – Vérifications ELU

Un chariot palan monorail est un système de manutention constitué d’un palan électrique ou manuel monté sur un chariot qui se déplace le long d’une poutre de roulement unique. Ce type d’équipement, largement utilisé dans l’industrie pour le levage et le transport de charges légère, génère des sollicitations particulières sur la structure porteuse du fait de la concentration des efforts sur la semelle de la poutre.

L’objectif de cette fiche est de présenter les vérifications spécifiques aux poutres de chariots-palans monorails à l’état limite ultime (ELU). Elle s’appuie sur la partie 3 de l’Eurocode 1 et sur la partie 6 de l’Eurocode 3 et sur leurs annexes nationales. Les vérifications à l’état limite de service (ELS) feront l’objet d’une fiche technique séparée.

Nous supposons que la poutre est un profilé laminé à chaud de section transversale bi-symétrique en I ou en H.

Actions sur les monorails

Composante statique

Dans la plupart des cas, il est d’usage de ne considérer que des charges verticales sur la poutre de roulement, et des charges horizontales longitudinales. Ces dernières sont évaluées à 5% des charges verticales, voir paragraphe 2.5.1.2(1) de la NF EN 1991-3 [1].

Les charges horizontales transversales peuvent être négligées à la condition que les opérations de levage se fassent à l’aplomb de la poutre et que les vitesses de déplacement restent faibles.

Coefficient dynamique

En l’absence d’information dans les documents du marché ou dans la fiche technique du fabricant, il est admis d’appliquer un coefficient dynamique forfaitaire de 1,20 aux charges verticales.

Vérifications ELU

Semelle inférieure

Les vérifications au niveau de la semelle inférieure doivent être menées selon les règles présentées au paragraphe 6.7 de la NF EN 1993-6 [3]. Il s’agit de vérifications plastiques, tenant compte à la fois des contraintes induites par la flexion globale dans la poutre et des effets de groupes pouvant se développer lorsque les deux rangées de galets d’un chariot-palan sont proches l’une de l’autre.

La méthode de Delesques, présentée dans un article de la Revue Construction Métallique de 1978, était couramment utilisée pour vérifier la semelle inférieure des poutres de monorails. Cette méthode historique était basée sur une approche élastique. Depuis l’introduction de l’Eurocode 3, une approche plastique est privilégiée, conduisant à des résultats notablement différents et généralement plus économiques.

Le modèle analytique est analogue à celui d’un tronçon en T qu’on considère dans le calcul des assemblages, et suppose un comportement rigide-plastique.

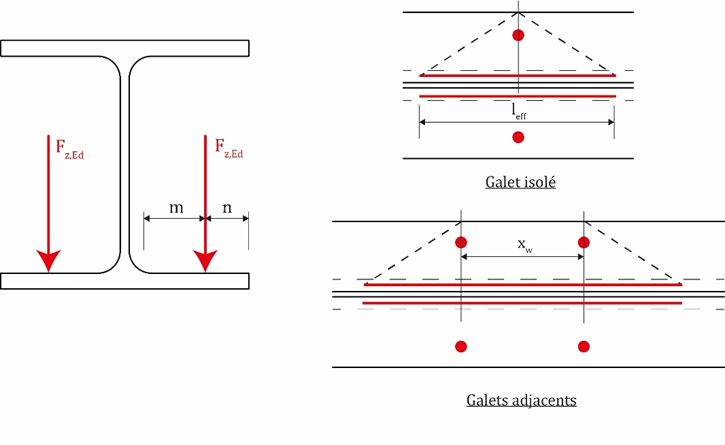
On évalue tout d’abord la charge de calcul au niveau d’un galet, notée, F_z,Ed, puis on la compare à la résistance calculée selon la formule suivante :

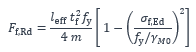
Avec :

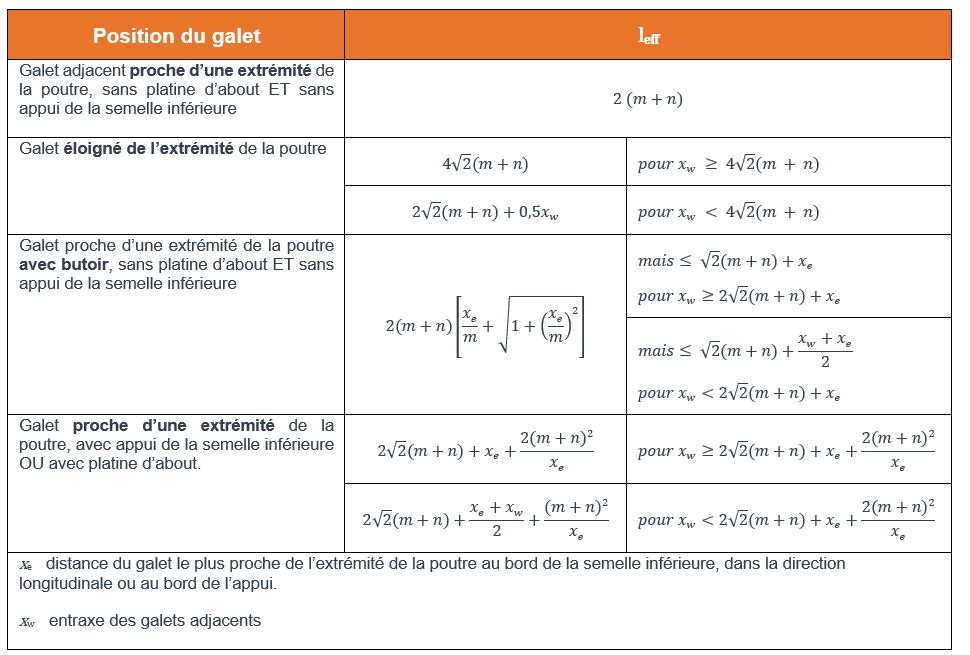
l_eff         longueur efficace de la semelle résistante déterminée à partir du tableau 6.2 de la NF EN 1993-6, en fonction des configurations étudiées : position du chariot sur la poutre, proximité des galets, etc.

m         bras de levier de la charge du galet par rapport au congé de raccordement de la semelle. Pour un profilé laminé :

t_f          Épaisseur de la semelle

t_w         Épaisseur de l’âme

r          rayon des congés

f_y          Limite d’élasticité de l’acier

γ_M0       Coefficient partiel qui vaut 1,0, voir [4].

σ_f,Ed      Contrainte de calcul au niveau de l’axe médian de la semelle provoquée par le moment de flexion globale.

Les longueurs efficaces ne sont pas les mêmes en fonction de la position de la section vérifiée. Il convient donc d’effectuer plusieurs vérifications le long de la poutre.

Jonction âme-semelle inférieure

En l’absence de formule d’interaction plastique, il convient d’effectuer une vérification de la semelle en évaluant une contrainte équivalente de von Mises en différents points.

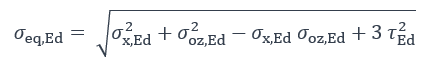
Avec :

σ_x,Ed        Contrainte globale, longitudinale, dans l’âme, au niveau du congé de raccordement,

σ_oz,Ed      Contrainte locale, transversale, dans l’âme, au niveau du congé de raccordement. Elle est évaluée en considérant une largeur de diffusion de πm.

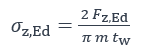
            Pour des galets adjacents, séparés par une distance inférieure à 0,5 πm il convient de tenir compte de la superposition des contraintes.

τ_Ed          Contrainte de cisaillement dans l’âme de la poutre.

La relation à vérifier est la suivante :

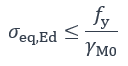
Déversement

Il convient de vérifier la résistance au déversement de la poutre en appliquant les méthodes présentées au paragraphe 6.3.2 de la NF EN 1993-1-1 [5]. La méthode simplifiée du paragraphe 6.3.2.4 peut être envisagée.

Notons que l’application des charges en partie inférieure du profil influence favorablement la résistance au déversement.

Les poutres de chariots-palans monorails sont généralement dépourvues de maintien entre appuis.

Références

[1]     NF EN 1991-3 : Eurocode 1 – Actions sur les structures. Partie 3 : Actions induites par les appareils de levage et les machines. AFNOR. Avril 2007.

[2]     NF EN 1991-3/NA : Eurocode 1 – Actions sur les structures. Partie 3 : Actions induites par les appareils de levage et les machines. Annexe Nationale à la NF EN 1991-3 :2007. AFNOR. Janvier 2010

[3]     NF EN 1993-6 : Eurocode 3 – Calcul des structures en acier. Partie 6 : Chemins de roulement. AFNOR. Septembre 2007.

[4]     NF EN 1993-6/NA : Eurocode 3 – Calcul des structures en acier. Partie 6 : Chemins de roulement. Annexe Nationale à la NF EN 1993-6 :2007. AFNOR. Décembre 2011.

[5]     NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.

[6]     NF EN 1991-3/NA : Eurocode 3 Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe Nationale à la NF EN 1993-1-1 :2005. AFNOR. Aout 2013

Télécharger le document

Romain Palacios, ingénieur de recherche, CTICM