Poutres de chariots-palans monorails – Vérifications ELS
Un chariot-palan monorail est un système de manutention constitué d’un palan électrique ou manuel monté sur un chariot qui se déplace sur la semelle inférieure le long d’une poutre de roulement unique.
L’objectif de cette fiche est de présenter les vérifications spécifiques aux poutres de chariots-palans monorails à l’état limite de service (ELS). Elle s’appuie sur la partie 3 de l’Eurocode 1 et sur la partie 6 de l’Eurocode 3 et sur leur annexe nationale. Les vérifications à l’état limite ultime (ELU) ont été traitées dans une fiche technique séparée.
Nous supposons que la poutre est un profilé laminé de section transversale bi-symétrique en I ou en H.
Actions sur les monorails
Composante statique
Comme expliqué dans la fiche technique consacrée aux vérifications ELU, les charges verticales et horizontales longitudinales (évaluées à 5% des charges verticales) constituent les sollicitations principales. En général, il n’y a pas lieu de prendre en compte d’actions perpendiculaires à l’axe de la poutre.
Coefficient dynamique
Comme pour les vérifications ELU, un coefficient dynamique forfaitaire de 1,20 est appliqué aux charges verticales. Ce coefficient intervient dans les combinaisons d’actions pour la résistance, il est ici utilisé pour le calcul des contraintes servant aux vérifications de réversibilité des déformations, considérée comme état limite de service.
Flèche
Les critères de flèche verticale et de déformation au niveau des appuis à respecter doivent être transmis par le client ou le fournisseur de l’équipement.
À titre informatif, le tableau 7.2 de l’annexe nationale de NF EN 1993-6 indique un critère de flèche verticale de L/500, pour un état limite de service, sans application des coefficients dynamique.
Les poutres de chariots-palans monorails peuvent être fixées à des traverses de l’ossature métallique. Dans ce cas, il est pertinent de vérifier que la déformation au niveau de l’appui ne soit pas trop importante au risque de gêner le fonctionnement de l’équipement. Il est prudent de s’assurer que le déplacement de l’appui ne dépasse pas le 500e de la plus petite portée des travées de poutre situées de part et d’autre de l’appui.
Réversibilité des déformations
Le comportement réversible de la section doit être assuré. Pour cela, il convient d’appliquer les règles exposées au paragraphe 5.8 et au paragraphe 7.5 de la NF EN 1993-6.
Les contraintes locales et globales doivent être évaluées en tenant compte des coefficients dynamiques.
Contraintes locales
Il convient de déterminer les contraintes dans la section au niveau de trois points d’intérêt : en sortie de congé de raccordement ⓪, sous le galet ① et en bord de semelle ②. Il y a 6 valeurs de contrainte locale à évaluer, 2 pour la flexion transversale et 3 pour la flexion longitudinale.
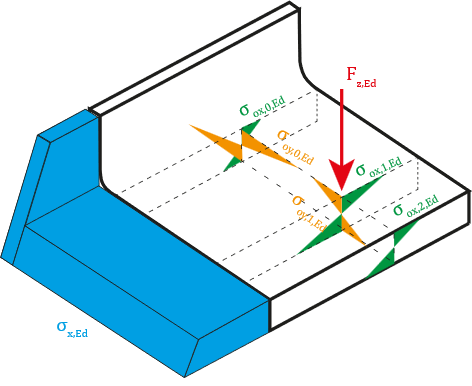
dans la semelle inférieure de la poutre
Les contraintes locales dépendent de la valeur de la charge au galet, de la position de la charge par rapport à l’extrémité de la semelle et de l’épaisseur de la semelle qui peut être constante ou variable.
Pour chacun des trois points d’intérêt, elles sont obtenues au moyen des formules suivantes :
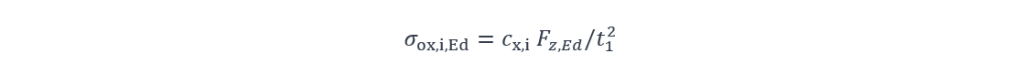
Et
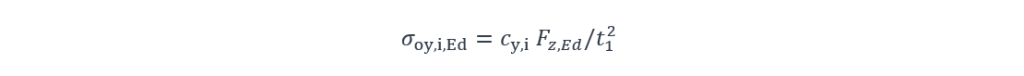
L’indice i fait référence aux points d’intérêt 0, 1 et 2.
Les formules des coefficients cx,i et cy,i du tableau suivant conduisent à des valeurs positives pour de la traction sur la face inférieure de l’aile et négatives pour de la compression. Pour la face supérieure, il convient de prendre ces coefficients avec le signe opposé.
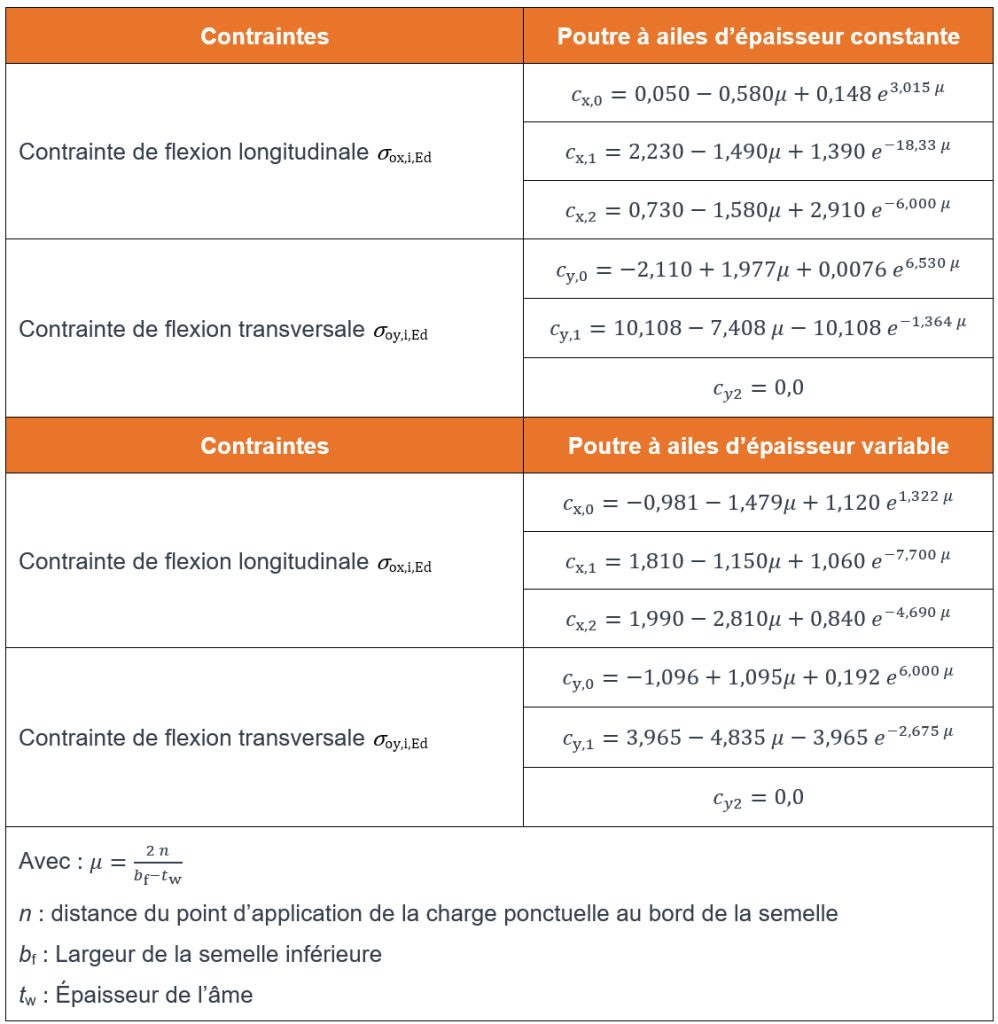
Dans le tableau précédent, les 6 premières formules correspondent au cas d’un profilé de type IPE ou HE, les 6 dernières couvrent le cas d’un IPN. Dans le domaine des poutres de chariots-palans monorails, il est encore courant d’utiliser de telles sections, l’inclinaison des ailes facilitant le fonctionnement de l’appareil de levage.
Les contraintes locales peuvent être déterminées à partir des formules analytiques présentées ci-dessus tant que la distance du galet à l’extrémité du profil, xe, est supérieure à la largeur de la semelle inférieure, bf.
Lorsqu’un galet se trouve à une distance xe inférieure à bf et que la semelle inférieure est soit posée sur un appui, soit soudée à un raidisseur d’extrémité reliant les deux semelles, alors ces formules peuvent toujours être appliquées.
En revanche, en l’absence de raidisseur ou d’appui de la semelle inférieure, il convient de négliger le comportement en plaque et d’évaluer uniquement une contrainte locale de flexion transversale à partir de la formule suivante :
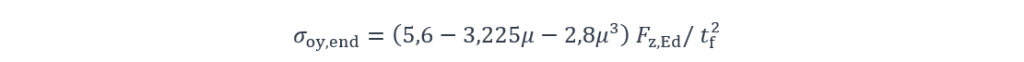
Cette formule conduit généralement à des niveaux de contraintes qui peuvent être élevés. Il devient alors nécessaire de renforcer localement la semelle inférieure par un plat soudé.
Le plat de renfort doit être soudé longitudinalement et transversalement à la section, et présenter une épaisseur supérieure ou égale à celle de la semelle de la poutre. La longueur de ce plat doit, quant à elle, être supérieure ou égale à la largeur de la semelle.
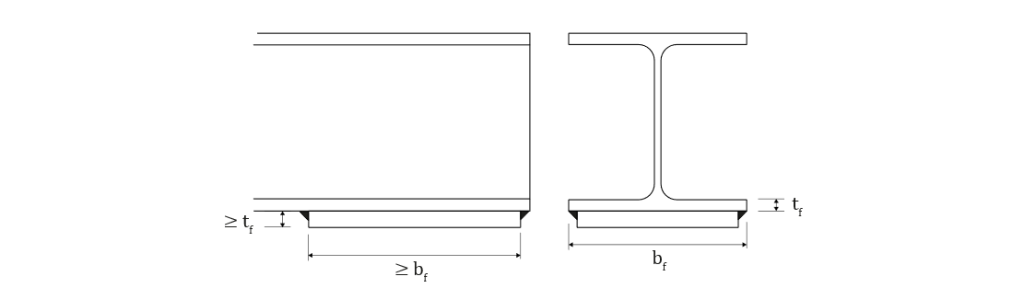
En présence d’un renforcement, la vérification du critère de réversibilité à l’extrémité de la poutre est couverte par le cas en partie courante, plus défavorable.
Dans le cas de galets adjacents, si l’entraxe des galets, xw, est inférieur à 1,15 bf, il convient de superposer les contraintes locales obtenues pour chacun des galets.
En alternative, il est possible de combiner les contraintes locales selon la méthode exposée dans l’Annexe Nationale britannique BS EN 1993-6/NA : 2007 [7] et reprise dans le projet de révision de l’EN 1993-6. La formule suivante est à appliquer pour chacun des trois points d’intérêt :

Avec :
c1 et c2 Paramètres de calcul définis comme suit :

σo1,i,Ed Contrainte locale de flexion, σox,Ed ou σoy,Ed, induite par un galet
σo2,i,Ed Contrainte locale de flexion, σox,Ed ou σoy,Ed, induite par deux galets
Contrainte équivalente
Les contraintes locales doivent être ensuite combinées aux contraintes globales afin d’évaluer une contrainte équivalente de von Mises. Cette contrainte équivalente est évaluée pour chacun des trois points d’intérêt et au niveau des faces inférieure et supérieure de la semelle inférieure au moyen de la formule générique suivante :
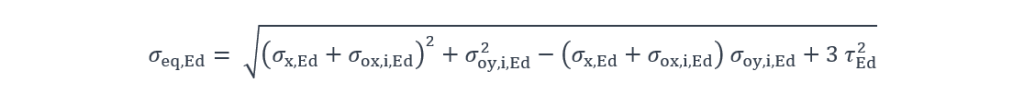
Avec :
σx,Ed Contrainte globale de flexion longitudinale dans la semelle, au niveau des fibres extérieures,
σox,i,Ed Contrainte locale de flexion longitudinale dans la semelle, au point i,
σoy,i,Ed Contrainte locale de flexion transversale dans la semelle, au point i,
t1 Épaisseur de la semelle au droit du galet.
Dans la plupart des cas, les niveaux de contrainte les plus élevés sont obtenus au point ①, sous le point d’application de la charge et au niveau de la face inférieure de la semelle.
Vérification
La condition à vérifier est la suivante :
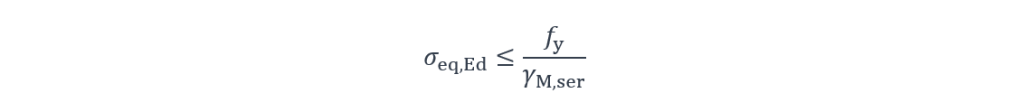
Avec :
γM,ser Coefficient partiel qui vaut 1,10 [4]
Références
[1] NF EN 1991-3 : Eurocode 1 – Actions sur les structures. Partie 3 : Actions induites par les appareils de levage et les machines. AFNOR. Avril 2007.
[2] NF EN 1991-3/NA : Eurocode 1 – Actions sur les structures. Partie 3 : Actions induites par les appareils de levage et les machines. Annexe nationale à la NF EN 1991-3 :2007. AFNOR. Janvier 2010
[3] NF EN 1993-6 : Eurocode 3 – Calcul des structures en acier. Partie 6 : Chemins de roulement. AFNOR. Septembre 2007.
[4] NF EN 1993-6/NA : Eurocode 3 – Calcul des structures en acier. Partie 6 : Chemins de roulement. Annexe nationale à la NF EN 1993-6 :2007. AFNOR. Décembre 2011.
[5] NF EN 1993-1-1 : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. AFNOR. Octobre 2005.
[6] NF EN 1991-3/NA : Eurocode 3 – Calcul des structures en acier. Partie 1-1 : Règles générales et règles pour les bâtiments. Annexe nationale à la NF EN 1993-1-1 :2005. AFNOR. Aout 2013
[7] BS EN 1993-6/NA : Eurocode 3 – Design of steel structures – Part 6: Crane supporting structures. UK National Annex :2007. BSI. 2013
Romain Palacios, ingénieur de recherche, CTICM