Constructions mixtes – Calcul des poutres de plancher mixte #5
Résistance à la flexion d’une poutre de plancher mixte – Section sous moment négatif : exemple d’application
Cet article fait suite à d’autres textes déjà publiés sur métalétech, que nous vous invitons à consulter pour une meilleure compréhension de celui-ci:
- Construction mixte acier-béton- Calcul des poutres de planchers #1 : largeur participante de la dalle à prendre en compte pour le calcul des poutres mixtes.
- Constructions mixtes – Calcul des poutres de planchers #2 : Résistance à la flexion d’une poutre de plancher mixte – Section sous moment positif
- Constructions mixtes – Calcul des poutres de plancher mixte#3: Section sous moment positif – Exemple d’application
- Résistance à la flexion d’une poutre de plancher mixte – Section sous moment négatif
Ce qui suit est un exemple d’application directe de l’article Résistance à la flexion d’une poutre de plancher mixte – Section sous moment négatif auquel vous devez vous reporter pour les explications théoriques, les notations et la démarche.
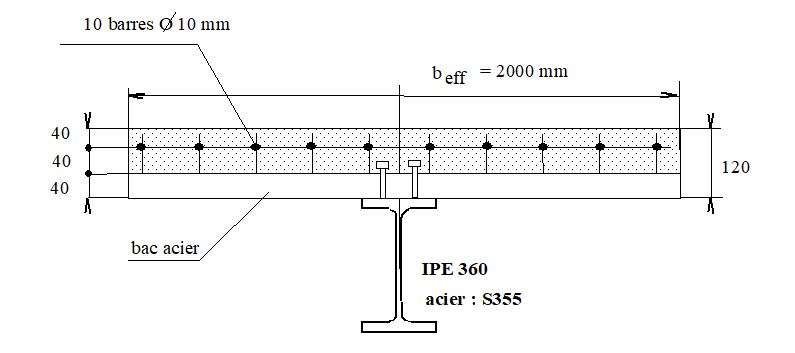
Données de l’exemple (figure 1)
La section ci-dessous est celle d’une poutre mixte continue au droit de l’appui intermédiaire.
L’armature longitudinale sur appui est constituée de 10 barres de diamètre 10 mm en acier B500H. Les armatures sont placées à une distance de 40 mm par rapport à la fibre supérieure de la dalle en béton. La largeur participante de la dalle est égale à 2000 mm.
On propose de calculer la résistance à la flexion de la section mixte fissurée et de comparer cette résistance à celle de la poutrelle métallique seule.
Calculs
Caractéristiques de la section acier seul (données à partir du catalogue fournisseur)
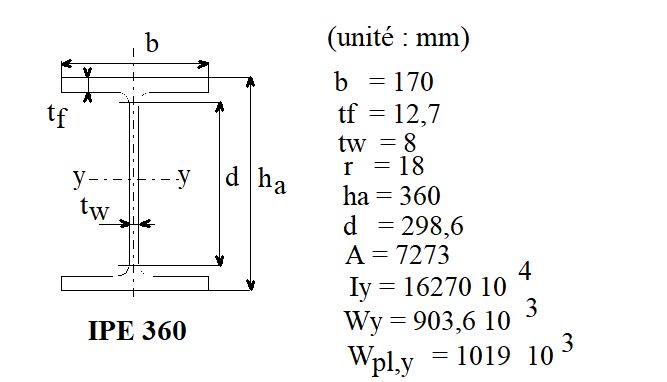
On se limite aux caractéristiques nécessaires pour le besoin de notre application.
Position de l’axe neutre plastique
FS = 10×78,5×500/1,15 = 341,3 kN
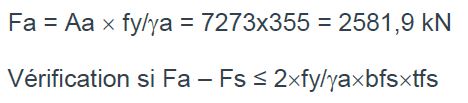
Fa – Fs = 2581,9 – 341,3 = 2240,6 kN
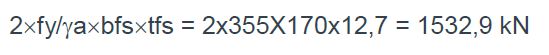
2240,6 > 1532,9 l’axe neutre plastique est dans l’âme
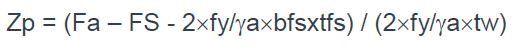
Zp = (2581,9 – 341,3 – 1532,9)x1000 / (2x355x12,7)
Zp = 707,7×1000 / (2x355x12,7) = 78,5 mm
Zp = 78,5 mm cette valeur est inférieure à 167,3 mm (360/2 – 12,7) nous pouvons donc appliquer l’expression donnée dans l’article cité en préambule à condition de vérifier la classe des sections.
Semelle
C/t = (170/2 – 4 – 18) / 12,7 = 4,96 la semelle est de classe 1
Âme
Hauteur de la partie droite de l’âme d = 298,6 mm
Hauteur de la partie droite comprimée de l’âme 298,6 – (78,5 -18) = 238,1 mm
α= 238,1/298,6 = 0,8
Limite classe 1 = 396×0,81/(13×0,8 –1) = 34,1
d/tw = 298,6/12,7 = 37,3 > 34,1 l’âme n’est pas de classe 1
Limite classe 2 = 456×0,81/(13×0,8 –1) = 39,3
d/tw = 298,6/12,7 = 37,3 < 39,3 l’âme est de classe 2
nous pouvons donc appliquer l’expression donnée dans l’article cite en préambule :
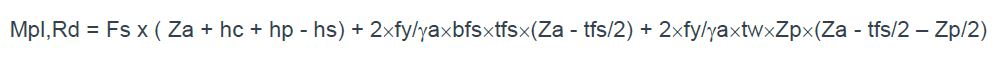
= 341,3 x (180 + 80 + 40 -40) + 1532,9x(180-12,7/2) + 707,7x(180-12,7/2 – 78,5/2)
= 341,3×260 + 1532,9×173,65 + 707,7×128,05
= (2581,9 – 341,3 – 1532,9)x1000 / (2x355x12,7) = 445,55 kN.m
La section mixte résistante à un moment de flexion négatif égal à Mpl,Rd = 445,55 kN.m
Moment résistant de la poutrelle acier seul = 1,019´355 = 361,75 kN.m
Comparaison
Moment résistant mixte / Moment résistant acier = 445,55 / 361,75 = 1,23
Le gain est appréciable mais très modeste par rapport aux sections mixtes sous moments positifs
Télécharger le document complet
Daniel Bitar, directeur du département études , CTICM