Calcul statique des câbles inextensibles de grand élancement géométrique

Cet article présente un formulaire de calcul statique d’un câble inextensible fixe à ses deux extrémités.

Les câbles sont utilisés dans de nombreuses industries : génie électrique, transport, génie civil, etc. Un câble est un élément long dont le comportement est non linéaire. Il possède une grande résistance à la traction. En revanche, ses résistances à la compression et à la flexion sont considérées comme négligeables. La déformée du câble après chargement étant souvent très différente de celle de la forme initiale, il convient d’effectuer les calculs en tenant compte du comportement non linéaire géométrique.

Les règles de calcul classiques utilisées en résistance des matériaux ne peuvent pas être directement appliquées aux câbles. C’est la raison pour laquelle cet article propose des formules analytiques permettant d’effectuer un calcul statique des câbles inextensibles et fixes à ses extrémités, en adoptant certaines hypothèses simplificatrices.

Hypothèses simplificatrices

Les formules de calcul dans cet article sont valables uniquement en adoptant les hypothèses suivantes :

• Parfaite flexibilité : cette hypothèse impose que le moment fléchissant est nul en tout point du câble ;
• Inextensibilité : la variation de la longueur du câble due à l’élasticité du matériau constitutif et à la variation de la température n’est pas considérée. Cet aspect pourra faire l’objet d’un autre article ;
• Chargement : le câble est soumis à une charge uniformément répartie sur sa longueur, le long de la corde reliant les deux extrémités du câble ;
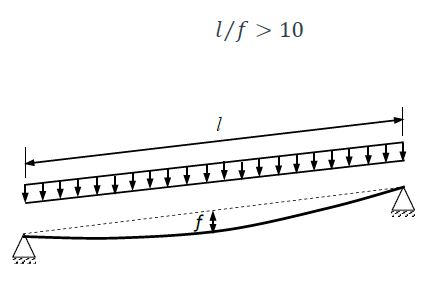
• Grand élancement géométrique l/f : lorsque l’élancement l/f est grand, la géométrie du câble peut être assimilée à une parabole. Plus le rapport l/f  est faible, plus sa géométrie s’éloigne d’une parabole. Dans ce cas, la géométrie du câble doit alors être représentée par une chaînette qui est bien évidemment plus complexe que la parabole. L’article [2] a montré que le cas de charge uniformément répartie par unité de longueur le long du câble est équivalent à ceux de charge uniformément répartie par longueur le long de la corde reliant les deux extrémités du câble.
• Il est admis qu’un câble est considéré comme élancé si l’élancement géométrique vérifie la condition suivante :

Notations

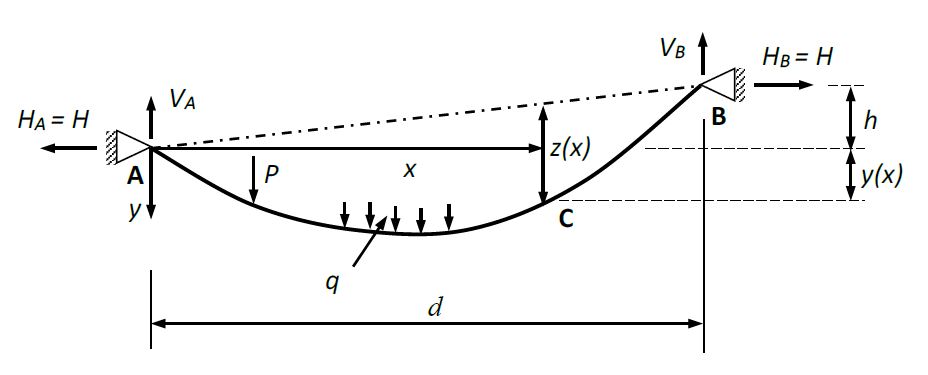
       d portée horizontale du câble

       L longueur développée du câble

       h différence de niveau entre les points d’ancrage

       l distance entre points d’ancrage :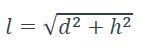

      H réaction d’appui horizontale

        f flèche du câble à mi-portée

      q_p charge répartie par unité de longueur horizontale : q_p=q l/d

Formulaire de calcul pour un câble inextensible soumis à une charge répartie

• Réaction horizontale :

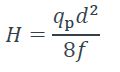
• Réaction verticale de l’appui gauche :

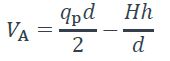
• Réaction verticale de l’appui droit :

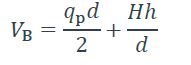
• Longueur développée :

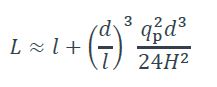
• Tension maximale :

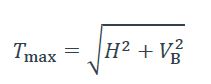
Exemple d’application

Données :

Condition de grand élancement géométrique du câble :

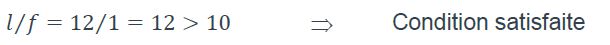
Charge répartie par unité de longueur horizontale :

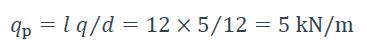
Réaction d’appui horizontale :

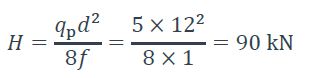
Réaction verticale de l’appui gauche :

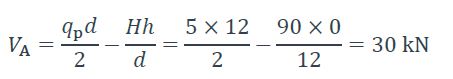
Réaction verticale de l’appui droit :

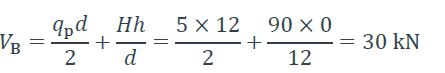
Longueur développée :

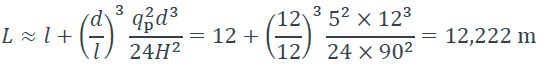
Tension maximale :

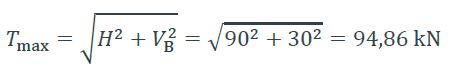
Cette valeur de tension maximale permet de choisir, pour une étude d’avant-projet la section droite du câble.

Références

[1]     NF EN 1993-1-11 – Eurocode 3 « Calcul des structures en acier » – Partie 1-11 « Calcul des structures à câbles ou éléments tendus ». AFNOR. Avril 2007.

[2]     T.M. Nguyen, « Formulaire de calcul statique des câbles », Revue construction métallique, N°2-2015.

Télécharger le document

Tien Minh Nguyen, chef de projet recherche– CTICM